問 題：

（１）　１，２，３，４ の数字だけを使って４桁の数を作る場合の数は？
（２）　１，２，３，４ の数字だけを使って、 またこれらの数を全て使って４桁の数を作る場合の数は？
（３）　１，２，３ の数字だけを使って、 またこれらの数を全て使って４桁の数を作る場合の数は？


　　　　　　　

（１） の解答

　 まず、 のＡ に当てはめる数字の数は４個、 その上で次にＢ に当てはめる数字の数は４個 、 その上で次にＣ に当てはめる数字の数は４個、 その上でＤ に当てはめる数字の数は４個である。 したがって、 場合の数は、 ４ × ４ × ４ × ４　＝→　256 とおり　である。

（２） の解答

　 まず、 のＡ に当てはめる数字の数は４個、 その上で次にＢ に当てはめる数字の数は３個、 その上で次にＣ に当てはめる数字の数は２個、 その上でＤ に当てはめる数字は自動的に決まる。 したがって、 場合の数は、 ４ × ３ × ２　＝→　24 とおり　である。

（ 別 解 ）

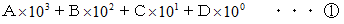
　 まず、 １ を Ａ 〜 Ｄ のどれかに入れる方法は４通り、 その上で２ を Ａ 〜 Ｄ のどれかに入れる方法は３通り、 その上で３ を Ａ 〜 Ｄ のどれかに入れる方法は２通り、 その上で４ がどこに入るのかは自動的に決まる。 したがって、 場合の数は、 ４ × ３ × ２　＝→　24 とおり　である。

（３） の解答

　 ３種類の数字のうち１種類だけ２回使わなければならないので、 その数字の選び方は３通りある。 １回だけ使われる数字は２種類であるが、 そのうちの１つを の Ａ 〜 Ｄ のどれかに入れる方法は４通り、 その上でもう１つの数字を Ａ 〜 Ｄ のどれかに入れる方法は３通り、 その上で２回使われる数字がどこに入るのかは自動的に決まる。 したがって、 場合の数は、 ３× ４ × ３　＝→　36 とおり　である。