非周期関数 f ( t ) の 複素フーリエ展開 （ 逆フーリエ変換 ）に似た式：

　　　
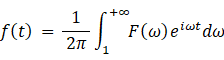
　　　　　　ただし、
　　　　　　　　　
　　　　　　　　　
　　　　　　　　　　　　　　

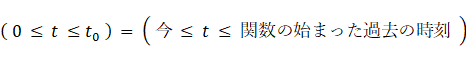
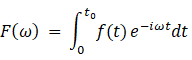
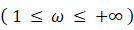
　e ^iωt は、複素平面において原点を軸に時計回りに角速度の大きさ ω で回転するベクトルを表します。

　この式は、原点の媒質分子の変位を、 0 ≦ t ≦ t₀ の範囲内のある時刻 t において、 1 ≦ ω ≦ ＋∞ のすべての角速度 ω における回転複素ベクトルの総和として表したものです。

　フーリエ変換によく似た式 F ( ω ) を「 フーリエ変換まがい 」と言うことにしましょう。フーリエ変換まがいは、周期 2π / ω 秒 の回転複素ベクトルの大きさ（ スペクトラム ）を表します。