【 問 題 】
-
簡略化のためにSI単位の記述を省略する。
質量 m の重りに長さ r のひもを付け、他の端を固定し、自由に振り子運動や非等速円運動ができるようにした。
重りの最下点において初速 v0 を与えるとき、非等速円運動にするためには v0 を最低でもいくらにしなければならないか?
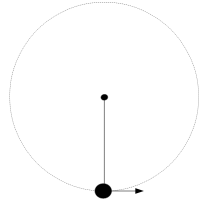
-
非等速円運動にするための必要条件は、重りが最上点にあって速さ v で移動しているときにひもが重りを引っぱる張力 ( T ) が0以上になっていることです。つまり、次の式が成り立っていることです。
T ≧ 0 ・・・ ①
重りが最上点にあって速さ v で移動しているときには、重りと並走している観察者にとって、次の力のつり合いの式が成り立っています。
mg + T = mv2/ r ・・・ ② ( 右辺は上向きの力で遠心力 )
重りが最下点にあって速さ v0 で移動しているとき と 重りが最上点にあって速さ v で移動しているとき のエネルギー保存則は、次の様になります。
1/2 × mv02 = 1/2 × mv2 + 2mg r ・・・ ③
③ より、
v02 = v2 + 4g r
よって、
v2 = v02 - 4g r ・・・ ④
② より、
T = mv2/ r - mg ・・・ ⑤
④ を ⑤ に代入して、
T = m ( v02 - 4g r ) / r - mg
よって、
T = ( m / r ) × ( v02 - 5g r ) ・・・ ⑥
⑥ を ① に代入して、
( m / r ) × ( v02 - 5g r ) ≧ 0
よって、
v02 - 5g r ≧ 0
よって、
v02 ≧ 5g r
よって、
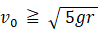
したがって答えは、
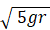
 力学 へ戻る
力学 へ戻る