【 問 題 】

半直線上を点Ｐが時刻 0 に原点を出発し次第に原点から遠ざかっていきます。
時刻 t における点Ｐの座標値を x とします。
時刻 t における点Ｐの移動の速さは次の式で与えられます。
　　
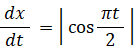
x を t を用いて表してください。

【 解 答 】

　　
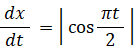
よって、
　　
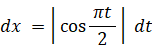
よって、
　　
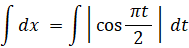
よって、
　　

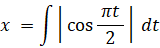
上式を解きます。
n を 1 以上の整数とします。
0 ≦ t　かつ　−1＋4n　≦　t　≦　1＋4n　のとき
　　
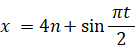
1＋4n　≦　t　≦　3＋4n　のとき
　　

【 考 察 】

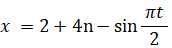
　t を 0 から 10 まで 0.1 ずつ増やしながら、x の位置に目盛りを付けます。そして、出来上がったのは、10 cm の目盛りの間隔が周期的に変化するスケールのようなものです。この線分は密度が周期的に変化しています。 t が偶数の周辺では粗になっていて、 t が奇数の周辺では密になっています。
　　
　　＜ 上図を描く十進BASIC のプログラム ＞
　　SET WINDOW -0.1,10.1,-3,3
　　SET LINE COLOR "Black"
　　SET LINE width 2
　　PLOT LINES: 0,0;10,0
　　SET LINE width 1
　　FOR n=0 TO 2
　　　FOR t=0 TO 10 STEP 0.1
　　　　IF -1+4*n < t AND t < 1+4*n THEN
　　　　　PLOT LINES: 4*n+SIN(t*PI/2),-1;4*n+SIN(t*PI/2),1
　　　　END IF
　　　　IF 1+4*n < t AND t < 3+4*n THEN
　　　　　PLOT LINES: 2+4*n-SIN(t*PI/2),-1;2+4*n-SIN(t*PI/2),1
　　　　END IF
　　　NEXT t
　　NEXT n
　　END


　密度が一定でない数直線はスケールとしては使えません。密度が一定でない直線は、いわば水平方向に歪んだ直線です。一方、直線がそれと垂直な方向にさまざまに歪んだものは曲線であり、曲線は２次元です。これを平面に応用してみます。密度が一定でない平面（ x 軸方向 と y 軸方向 にそれぞれ歪んだ平面 ）は、いわば水平方向に歪んだ平面です。一方、平面が x 軸 かつ y 軸 に垂直な方向にさまざまに歪んだものは曲面であり、曲面は３次元です。では、これを空間に応用してみてください。 x 軸方向、 y 軸方向、 z 軸方向 にそれぞれ歪んだ空間は３次元で、こららの３軸とすべて垂直な方向に歪んだ空間は４次元です。