力学 へ戻る（１） 宇宙的に見たフーコーの振り子の動き
-
北極点の真上の空間に常に存在していて自転していない観察者Ａ君がいます。 彼から見るとフーコーの振り子はどのように運動するのでしょうか？ いろんなケースを考えてみましょう。
北極点に立てた家の天井の真ん中を支点とする振り子は、 Ａ君から見ると、 振り子の支点も振り子の軌道 （ 直線分と見なすことができる ） も共に静止したままです。 一方、 家からすると、 振り子の支点は静止したままで、 振り子の軌道は地軸を軸とする回転 （ 周期24時間 ） をします。
赤道上に立てた家の天井の真ん中を支点とする振り子が最初東西方向に振動しています。 Ａ君から見ると、 振り子の支点も振り子の軌道も地軸を中心とする等速円運動 （ 周期24時間 ） をします。 一方、 家からすると、 振り子の支点も振り子の軌道も静止したままです。
赤道上に立てた家の天井の真ん中を支点とする振り子が最初南北方向に振動しています。 Ａ君から見ると、 振り子の支点も振り子の軌道も地軸を中心とする等速円運動 （ 周期24時間 ） をします。 一方、 家からすると、 振り子の支点も振り子の軌道も静止したままです。
北緯45度上に立てた家の天井の真ん中を支点とする振り子が最初東西方向に振動しています。 Ａ君から見ると、 振り子の支点も振り子の軌道も地軸を中心とする等速円運動 （ 周期24時間 ） をします。 一方、 家からすると、 振り子の支点は静止したままで、振り子の軌道は地球の中心と家とを結ぶ直線を軸とする回転をします。次のような回転です。
※ 角速度 ＝ sin(45度) × 360度 / 24時間
ではこれから、 Ａ君から見える北緯45度上にあるフーコーの振り子の軌道の前後方向 （ 最初は東西方向で非前後(非南北)方向です。） について解説します。 振り子運動の東側の折り返し点をＡ点とし、 西側の折り返し点をＢ点とします。 振り子の軌道は微小土地部分に対して時計回りに回転しますので、 最初の約17時間は点Ａは点Ｂよりも地軸に対して遠い所を回転しますが、 その後の17時間は近い所を回転します。このとき、 最初の約17時間は点Ａは点Ｂよりも遠い所にありますが、 その後の17時間は近い所にあります。
以上の考察より、 私の言いたいことは次のことです。 Ａ君から見て、 振り子が北極点にあるとき や 赤道上にあって南北方向に振動しているとき には、 振り子の軌道の方向は 前後(南北)方向 には不変ですが、 そうでないときは振り子の軌道は前後(南北)方向を変えるのです。 ですから、 フーコーの振り子のしくみを説明するのに、 安易に考えて、「 振り子の軌道の方向は不変であるが、 地面が回転するので、 相対的に振り子の軌道が回転するのである。」と、 間違ったことを言ってはならないということです。
-
振り子の軌道は地球の自転の影響を受けないのではなく、 地球の自転による振り子の軌道の回転は、 ある特定の方向のみ地球の自転の影響を受けません。
地球上の微小土地部分は、 中心を通る地軸に平行な軸を中心に角速度の大きさ 約
で自転しているわけですが、 これを「 微小土地部分から鉛直に伸びた直線を中心とする回転（ 垂直軸自転 ）」と「 微小土地部分から真北に伸びた直線を中心とする回転（ 水平軸自転 ）」とに分解することができます。 そのとき、 北緯 θ 度にある微小土地部分の角速度の大きさは、 前者は 
で、 後者は 
です。 微小土地部分に設置されたフーコーの振り子の軌道の回転運動は、「 微小土地部分から鉛直に伸びた直線を中心とする回転（ 垂直軸自転 ）」と「 微小土地部分から真北に伸びた直線を中心とする回転（ 水平軸自転 ）」とに分解された後、 前者は消滅します。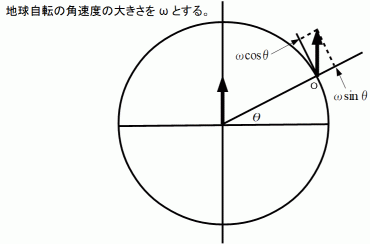
フーコーの振り子の仕組みは、 次の文章です。
フーコーの振り子は、 地球上の微小地面の北極星に向かう方向への自転の角速度（ 大きさは 2π rad/day ） の鉛直成分の大きさ を測る道具である。
※ 水平成分は 真北に向かう方向です。
フーコーの振り子については、 自転の鉛直成分が消失するために、 地球上の微小土地部分の自転の鉛直成分が相対的に観察されるのである。 つまり、 フーコーの振り子の軌道が鉛直軸を中心に自転しているのではなく、 観察者の立っている地面が鉛直軸を中心に自転しているのである。 なお、 フーコーの振り子の軌道の北向きの水平軸を中心とする自転は、地球上の微小土地部分の北向きの水平軸を中心とする自転と全く同じある。
※ 水平成分は 真北に向かう方向です。
フーコーの振り子については、 自転の鉛直成分が消失するために、 地球上の微小土地部分の自転の鉛直成分が相対的に観察されるのである。 つまり、 フーコーの振り子の軌道が鉛直軸を中心に自転しているのではなく、 観察者の立っている地面が鉛直軸を中心に自転しているのである。 なお、 フーコーの振り子の軌道の北向きの水平軸を中心とする自転は、地球上の微小土地部分の北向きの水平軸を中心とする自転と全く同じある。
-
実験 Ａ ：
-
地球儀を北極点が真ん中に見えるような位置から眺め、 一周する緯線たちに注目してください。 まず、 竹ヒゴを赤道面と平行にしたら、赤道に接するようにし、 赤道の曲率半径を考えます。 竹ヒゴはフーコーの振り子の軌道の運動方向を表します。 次に、 竹ヒゴを北緯40度の緯線に接するようにし、 緯線の曲率半径を考えます。 その次に、 竹ヒゴを北緯80度の緯線に接するようにし、 緯線の曲率半径を考えます。 すると、 北極点上では緯線の曲率半径は ０ で、 赤道の曲率半径は地球の半径に等しいことが判ってくると思います。
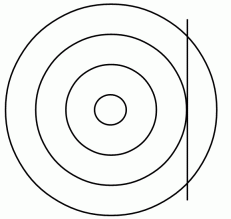
今度は、 地球儀の北極点を左側にして赤道が真ん中に見えるような位置から地球儀を眺めます。 それから、 竹ヒゴを赤道面と平行にしたら、 赤道に接するようにし、 赤道の曲率半径を考えます。 立体的にイメージしてください。 やはり、 赤道の曲率半径は地球の半径に等しいことが判ります。
以上より、 フーコーの振り子の軌道の回転の速さを表す角速度の大きさ （ 度/日 ） は次の式で与えられるのではないかと推定されます。
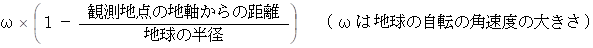
しかし、 この式は間違いです。 なぜなら、 そもそもフーコーの振り子の軌道の回転のイメージが間違っているからです。 ちなみに、 正解は ω sin θ です。
実験 Ａ における竹ヒゴは、緯線で切断した地球の断面を含む平面上の直線です。これはフーコーの振り子の軌道が描く線分が乗っかる直線ではありません。
-
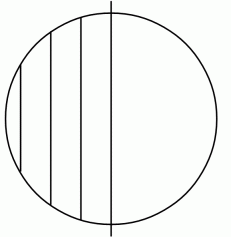
次に、 北緯40度の緯線上の１点が地球儀の真ん中に見えるようにして、 そこに竹ヒゴが接するようにしてから緯線の曲率半径を考えます。
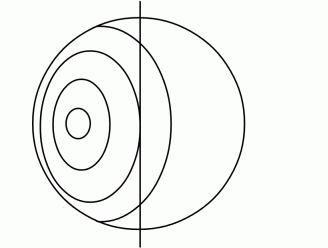
これこそが、 フーコーの振り子の軌道の回転のイメージです。
実験 Ｂ における竹ヒゴは、地球の中心を通る断面を含む平面上の直線です。これがフーコーの振り子の軌道が描く線分が乗っかる直線です。
-
地球が自転しているために、地球外の北極の真上に存在する観察者にとっては、地球の微小面積地面は北極を中心にして１日で反時計回りに １回公転 １回自転 しています。地球の微小面積地面の自転は「 微小土地部分から鉛直に伸びた直線を中心とする回転（ 垂直軸自転 ）」と「 微小土地部分から真北に伸びた直線を中心とする回転（ 水平軸自転 ）」とに分解されます。
フーコーの振り子のしくみの説明に次のようなものがあります。
-
振り子の振動方向は地球の自転の影響を受けないので、地球の外から振り子を観察すると常に一定の方向に振動しています。したがって、本当は地面が回転しているのですが、フーコーの振り子の軌道が回転しているように見えるのです。
北緯30°の地面は１日で sin 30°回「 微小土地部分から鉛直に伸びた直線を中心とする回転 」をし、cos 30°回 「 微小土地部分から真北に伸びた直線を中心とする回転 」をしているのです。 sin 30°＝ 0.5 cos 30°≒ 0.866 です。
北緯30°の地面に寝転んでいる人が、昼間も恒星が見えるものとして、１日間ずっと北極星を中心とする天体を観察すると、恒星たちは北極星を中心に１回転します。ということは、北緯30°の地面は１日で１回自転しているということです。北緯30°の地面にいる人は、その人と北極星を結ぶ直線を軸にして１日間に１自転しているのですが、その内訳は、１日に 0.5 回の「 微小土地部分から鉛直に伸びた直線を中心とする回転（ 垂直軸自転 ）」と １日に 0.866 回の「 微小土地部分から真北に伸びた直線を中心とする回転（ 水平軸自転 ）」になります。 0.5 2 ＋ 0.866 2 ≒ 1 です。