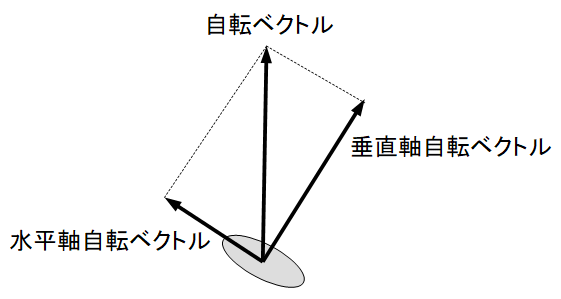
フーコーの振り子は特殊で「 回転ベクトルの分解法則 」が成り立ちません。振り子を支える脚はちゃんと回転ベクトルの分解法則に従うのですが、振り子の軌道はそれに従わないのです。「 地球の自転に由る振り子の軌道の自転 」を表す自転ベクトル（ 北極星向き ）を垂直な２方向に分解したとき、その「 北向き水平軸の分解自転ベクトル（ 水平軸自転ベクトル ）」はそのまま保たれるのですが、「 天頂向き鉛直軸の分解自転ベクトル（ 垂直軸自転ベクトル ）」は消失するのです。そのために振り子の脚が設置された局所地面の垂直軸自転ベクトルで表される自転運動が相対的にあらわになるのです。

　普通の直進ベクトルは、力のベクトルや速度のベクトルのように直線的なイメージで、向きと大きさを表します。回転ベクトルも同様に１本の矢印で表現され、方向と大きさの情報を持ちます。矢印の向きが右ネジの法則に従う回転の向きを表し、矢印の長さが角速度の大きさを表すのです。例えば、地球の自転を表す回転ベクトルは、地球の中心から北極星向きであり、角速度360度/日に相当する長さになっています。また、地球の表面の局所地面の自転は、地球の自転を表す回転ベクトルと同じ回転ベクトルで表されます。

　この局所地面の自転ベクトルは水平軸自転ベクトルと垂直軸自転ベクトルとに分解することができます。例えば北緯60度にある局所地面は、角速度 360度×cos(60度)/日 に相当する長さの水平軸自転ベクトルと角速度 360度×sin(60度)/日 の長さに相当する垂直軸自転ベクトルとに分解することができます。したがって、赤道上の局所地面は 360度/日 の角速度で北向き水平線を軸に反時計回りに水平軸自転のみしていて、北極点上の局所地面は 360度/日 の角速度で天頂向き鉛直線を軸に反時計回りに垂直軸自転のみしていて、北緯60度にある局所地面は 360度×cos(60度)/日 の角速度で北向き水平線を軸に反時計回りに水平軸自転しながら、360度×sin(60度)/日 の角速度で天頂向き鉛直線を軸に反時計回りに垂直軸自転していることになります。

　実は、フーコーの振り子の垂直軸自転ベクトルが消失しているのではありません。振り子の糸の運動が作る軌道面、それは地球の重心を通る断面上にあるのですが、不変を保とうとして、地球の自転によるその断面の移動に従わず、地球の重心を通る断面を乗り換え続けているのです。

　フーコーの振り子は、地球の自転を証明し、リューヴィルに回転ベクトルやその分解法則を発見させたのです。

※ 追伸：
　　　微小局所平面の公転は、微小局所平面の重心の移動形態の１つです。
　　　微小局所平面の自転は、微小局所平面の重心を通る軸を中心とする回転です。

　　

※ 参考：
　　　剛体力学 ＞ 剛体の自転の４大原理
　　　大学生のための数学 ＞ その他の数学 ＞ ３次元空間における微小局所平面の回転運動
　　　ばいおりんの日常的物理学文集 ＞ 天文学と物理学 ＞ 地面の公転と自転