点Pは半径 r m の円の円周上を角速度の大きさ ω rad/s で反時計回りに等速で回転しています。
時刻 t s = 0 s のとき、点Pの位置ベクトルは( r , 0 )です。
時刻 t s における点Pの位置ベクトルを複素ベクトルで表すと、次のようになります。
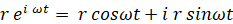
等速円運動をしている点Pの速度は次のようになります。
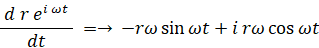
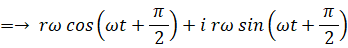
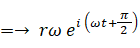
等速円運動をしている点Pの加速度は次のようになります。
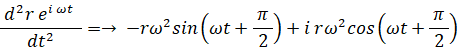
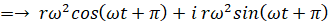
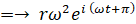
なお、等速円運動における 速さ ( v m/s ) と 角速度の大きさ ( ω rad/s ) の関係は次の式で表されます。
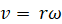
 解析学 へ戻る
解析学 へ戻る