複素数 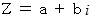：　　の絶対値は次の式で表されます。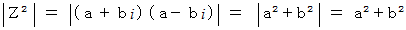
　　　　


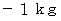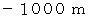　 さて、「 の水を加える。」場合の、 加える量は です。「 東へ移動する。」場合の、 移動する量は 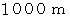です。 前者の量は負の数であり、 後者の量は正の数です。

　 後者のような数直線の場合の負の記号は、 量を表すものではなく方向を表すものですから、 本来なら、 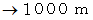とか 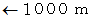とかで表さなければならないところを、 古くからの習慣で、 本来は量を表す 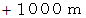とか とかで表しているので、 次のような事実が覆い隠されてしまっています。

　 どんな前提があったとしても、 物理学上は 東に移動することはできますが、 最初の水の質量が 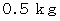の場合は、 物理学上は 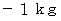の水を加えることはできません。

　 数直線の場合は、 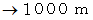とか 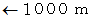とかの表現を用いることにしてはどうでしょうか。


　 前置きはこのくらいにして、 今日の本題に入ります。 複素数は、 ２次元の方向と量を持つ空間ですので、 複素数の「 大きさ 」を表す場合には、 数直線の量と同じように必ず正の数が用いられます。 複素数の大きさは、 ２次元ベクトルの大きさに似ています。 複素数の「 大きさ 」のことは「 絶対値 」と言われていますが、「 複素数の絶対値 」という言葉を止めて「 複素数の大きさ 」という言葉を使うようにしてはどうでしょうか。