関数とは何? と聞かれれば、 それは対応ですと答えます。 あるものを、 関数器にインプットすると、 別のものがアウトプットされます。 関数とは、 インプットされるものとアウトプットされるものとの対応です。
インプットされるものとアウトプットされるものが明白である場合、 観察と実験によって、 関数器のしくみを解明していくというのが、 ニュートン力学や熱力学や電磁気学のやり方です。「 事件は会議室で起こっているんじゃない!」です。 こうして、 ブラックボックスであった関数器のしくみが解明され、 自然の法則が発見されてきました。 ケプラーの法則、 万有引力の法則、 マクスウェルの法則、 電磁誘導の法則 などは関数です。 一方、 相対性理論では、 インプットされるものとアウトプットされるものが明白でないため、「 思考実験 」という形式で関数器のしくみを発見していきます。「 事件は会議室で起こっている。」のです。
演算子も関数の一種です。「 狭義の関数 」と演算子の違いは、 関数器が動くのか、 それとも、 インプットされる物が動くのかの違いです。「 狭義の関数 」は、 食虫植物ウツボカズラの捕虫器に例えられます。 インプットされるものは滑り落ちる昆虫です。 演算子は、 レンゲの花の蜜を吸うミツバチに例えられます。 インプットされるものは蜜です。
「 狭義の関数 」のイメージ :

演算子のイメージ:

関数器の分類 ;
 等価的対応をするもの
等価的対応をするもの国際空港に設置してある「 自動円ドル交換機 」
日本に過剰に存在する「 自動販売機 」
日英翻訳アプリケーションソフト
座標変換テンソル etc.
 加工的対応をするもの
加工的対応をするもの数学的関数
プログラミング関数
オートメーションの各種製造機
労働する人
写像テンソル etc.
 観測的対応をするもの
観測的対応をするもの量子力学的演算子 etc.
 別の関数にインプットされる 存在状態を表すもの
別の関数にインプットされる 存在状態を表すもの波動関数 etc.
量子力学になると、 関数は、 従来のブラックボックス的な関数 と 新しい虫眼鏡的な関数 とに分かれて行きます。 従来のブラックボックス的な関数といっても、 それは関数のイメージ「 対応 」とは随分とかけ離れた概念です。 その量子状態を表す波動関数は、 無次元の波動的ベクトル空間における関数です。 一方、 新しい虫眼鏡的な関数は、 概念としては従来のイメージであり、 量子力学的演算子 と言われます。 ボーッとした量子状態に、 演算子を作用させると、 はっきりとした物理量がアウトプットされ、 それによって、 ボーッとしたものの正体の一部が見えてきます。
物理学における演算子は、 行列の形をとることが多いです。 演算子としての行列 のことを、 私は「 空間的テンソル 」と言っています。 空間的テンソルには、 加工をして対応させる写像的なものと、 翻訳をして対応させる座標変換的なものとがあります。
前者の代表は、 電流に磁場演算子を作用させると導線に働く力 ( ローレンツ力 ) がアウトプットされるというものです。 フレミングの左手の法則です。 磁場演算子は、 外積演算子の形をとります。 つまり、 磁場を
 とすると、 磁場演算子は、 次のような行列になります。
とすると、 磁場演算子は、 次のような行列になります。
後者の代表は、 ローレンツ変換です。 ローレンツ変換は、 ニュートン力学的な時空間を相対論的な時空間に翻訳します。 ローレンツ変換は次のような行列をした空間的テンソルです。

量子力学以前は、 このようなブラックボックス的な演算子を発見することが物理学でしたが、 量子力学における演算子は、 ブラックボックス的な量子状態 ( 波動関数 ) を観測する道具として用いられます。 たとえば、 量子力学には次のような演算子があります。
エネルギー演算子 :


運動量演算子 :

運動エネルギー演算子 :

エネルギー演算子を量子状態 (
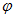 ) に作用させて、 エネルギーを観測することは、 次のように表現されます。
) に作用させて、 エネルギーを観測することは、 次のように表現されます。
 エネルギー演算子 :
エネルギー演算子 : の証明
の証明



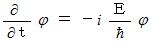

 運動量演算子 :
運動量演算子 :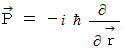 の証明
の証明

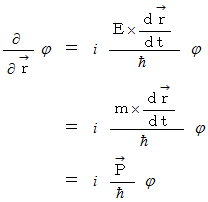


 運動エネルギー演算子 :
運動エネルギー演算子 : の証明
の証明

ただし、
 は、 ラプラシアン
は、 ラプラシアン
のことです。
 量子力学 へ戻る
量子力学 へ戻る