周期 T = 2π の周期関数は、次のようにフーリエ級数展開をすることができます。
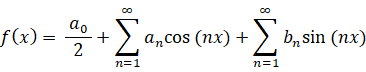 ・・・ ①
・・・ ①ただし、
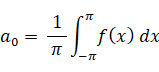 ・・・ ②
・・・ ②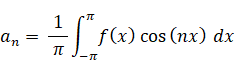 ・・・ ③
・・・ ③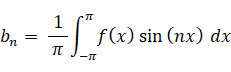 ・・・ ④
・・・ ④※ 三角関数は直交しているので、基底ベクトルのように扱うことができます。
( 参照 )
大学生のための数学 >その他の数学 > 周期関数の内積
大学生のための数学 > 線形代数学 > 2つの関数の正規相関関係
② ~ ④ は関数の内積であり、ある周波数の波がどれくらい含まれているのかを表します。
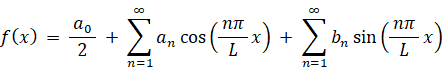 ・・・ ⑤
・・・ ⑤ただし、
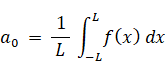
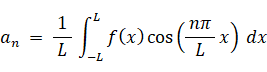
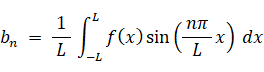
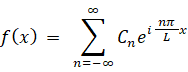 ・・・ ⑥
・・・ ⑥ただし、
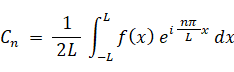
※ ⑥ は次の式たちを ⑤ に代入することによって導かれます。
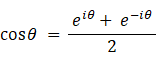
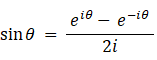
フーリエ級数は、周期関数を三角関数の和で表すものです。
複素フーリエ級数は、フーリエ級数を複素指数関数で表すものです。
フーリエ変換は、非周期関数も対象とする複素フーリエ級数のことです。
フーリエ変換( \( \omega \) の関数 ):
\( F\left(\omega\right)\ =\ \int_{-\infty}^{\infty}f\left(t\right)\ e^{-i\omega t}dt \)
※ ある周波数の波がどれくらい含まれているのかを表す。
逆フーリエ変換( \( t \) の関数 ):
\( f\left(t\right)\ =\ \frac{1}{\ 2\pi\ }\int_{-\infty}^{\infty}F\left(\omega\right)\ e^{i\omega t}d\omega \)
※ 原点の媒質分子のある時刻における変位を表す。
複素フーリエ級数は、フーリエ級数を複素指数関数で表すものです。
フーリエ変換は、非周期関数も対象とする複素フーリエ級数のことです。
フーリエ変換( \( \omega \) の関数 ):
\( F\left(\omega\right)\ =\ \int_{-\infty}^{\infty}f\left(t\right)\ e^{-i\omega t}dt \)
※ ある周波数の波がどれくらい含まれているのかを表す。
逆フーリエ変換( \( t \) の関数 ):
\( f\left(t\right)\ =\ \frac{1}{\ 2\pi\ }\int_{-\infty}^{\infty}F\left(\omega\right)\ e^{i\omega t}d\omega \)
※ 原点の媒質分子のある時刻における変位を表す。
 解析学 へ戻る
解析学 へ戻る