基礎物理学 へ戻る【 問 題 】
-
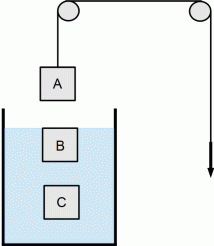
一辺の長さが 10 cm の立方体をした質量 8 kg の物質にロープを付け、 ２つの滑車を用いて吊るします。
物質がＡの位置にあり続けるためには、 ロープを 8
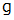N の力で引く必要があります。 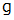は重力加速度です。水の密度を 1000 kg / m3 とします。 水槽に入っている水の量は １ m3 です。
では、 物質がＢの位置にあり続けるためには、 ロープを 何 N の力で引く必要がありますか？
また、 物質がＣの位置にあり続けるためには、 ロープを 何 N の力で引く必要がありますか？
-
浮力がかかる分、Ａの位置よりも小さな力ですみます。 浮力は水深に無関係ですので、 Ｂの位置 と Ｃの位置とで ロープを引く力は同じです。
浮力は、水に浸かった物質の体積に等しい水による重力量に等しいので、 次のようになります。
1000 kg / m3 × 0.001 m3 ×
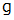m / s2 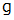＝→ kg・m / s2 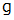＝→ Nしたがって、 答えは、 Ｂの位置 も Ｃの位置 も 7
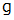N です。水圧 ＝ 水の密度 × 水深 × 重力加速度
水による浮力 ＝
− 
水中の物質の表面にかかる下向きの水圧を全表面について積分したもの_____ 水中の物質の表面にかかる上向きの水圧を全表面について積分したもの水の密度 ：
４℃のとき 999.7 kg / m3
20℃のとき 998.2 kg / m3
重力加速度 ：
9.80665 m / s2
浮力とは、気体や液体の中にある物質の表面の各部位がそれから受ける圧力の合力のことです。
浮力は物質の形や水深に無関係です。「 水面下の物質の体積 」は「 水で満杯の容器に物質を入れたときにあふれ出る水の体積 」ともいうことができます。 そこで、 水による浮力とは、「 あふれ出た水の質量に重力加速度をかけたもの 」 つまり 「 あふれ出た水の重量力 」であるということができます。 ( アルキメデスの原理 )
浮力は物質の形や水深に無関係です。「 水面下の物質の体積 」は「 水で満杯の容器に物質を入れたときにあふれ出る水の体積 」ともいうことができます。 そこで、 水による浮力とは、「 あふれ出た水の質量に重力加速度をかけたもの 」 つまり 「 あふれ出た水の重量力 」であるということができます。 ( アルキメデスの原理 )
水による浮力 ＝
− 水中の物質の表面にかかる下向きの水圧を全表面について積分したもの 水中の物質の表面にかかる上向きの水圧を全表面について積分したもの上記の式が成り立っていることを、 例を揚げて確かめてみましょう。
底面の半径と高さがともに １ m の 円錐 を底面が水深 １ m になるようにすっぽりと水の中に入れたとき、 下向きの水圧がかかる部分は側面であり、 上向きの水圧がかかる部分は底面です。
水の密度を 1000 kg/m3、 重力加速度を
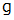とします。底面にかかる上向き水圧の積分は、 次のようになります。
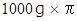
側面にかかる下向き水圧の積分は、 次のようになります。
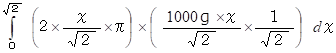
水圧は物質の表面に垂直な方向に作用しますので、
側面にかかる 水圧の水平方向成分 と 垂直方向成分 の大きさは等しくなっているからです。
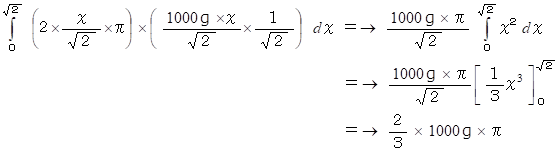
したがって、 水による浮力は次のようになります。
したがって、 次の式が成り立つちます。
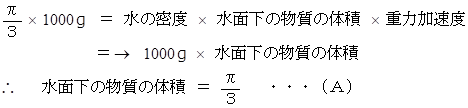
一方、 一般的には、 この円錐の体積は次のようにして求めることができます。
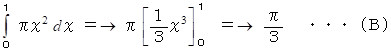
（Ａ）と（Ｂ）は、 等しくなっています。