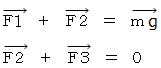

 を重りの重さ、
を重りの重さ、  を重りの速さ、
を重りの速さ、  を振り子の長さ とする。
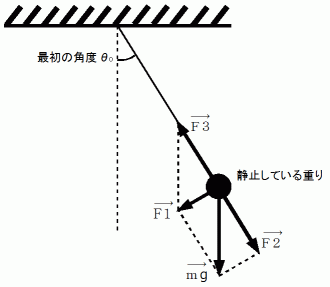
を振り子の長さ とする。実際に重りに作用している力は、
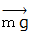 と
と 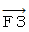 である。 この2つの力を合成すると、
である。 この2つの力を合成すると、 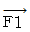 になる。
になる。 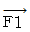 は単振り子の軌道の接線方向( 重りの移動の方向 )に作用している。
は単振り子の軌道の接線方向( 重りの移動の方向 )に作用している。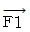 は、 折り返し点が最大で、 最下点が最小である。
は、 折り返し点が最大で、 最下点が最小である。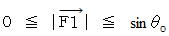
さて、 非等速円運動の 力の大きさ は、 次のように表される。
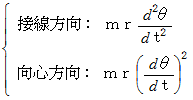
参考: 力学 > 円運動の運動方程式
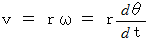 だから、 非等速円運動の 加速度 は次のように表される。
だから、 非等速円運動の 加速度 は次のように表される。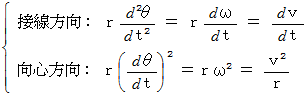
加速度の接線方向成分は、 速度の大きさの変化の度合いを表し、 加速度の向心方向( 法線方向 )成分は、 速度の向きの変化の度合いを表している。
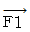 の大きさは次のように表される。
の大きさは次のように表される。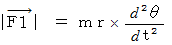
したがって、 次の式が成り立つ。
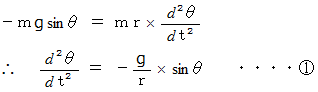
では、 この2階微分方程式を解いてみよう。 しかし、 これは楕円関数という高等技術を用いないと解けないそうなので、 振幅が微小であると仮定して、
 で近似する。
で近似する。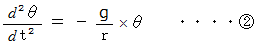
この式を「 単振動の運動方程式 」から導かれる次の「 単振動型2階微分方程式 」と比較すると、
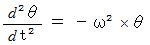
角振動数は、 次のようになる。
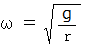
したがって、 周期
 は次のようになる。
は次のようになる。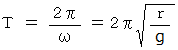
この結果より、 単振り子の周期は、 質量や振幅に関係なく、 紐の長さの平方根に比例することがわかる。
少し頑張って、
 を解いてみる。
を解いてみる。 と置くと、
と置くと、  は次のようになる。
は次のようになる。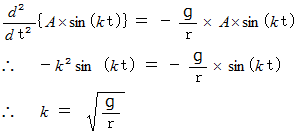
したがって、
 は次のようになる。
は次のようになる。
 を満たす。 この式から、
を満たす。 この式から、  は、 サインカーブのような時間を変数とする周期関数であることがわかる。
は、 サインカーブのような時間を変数とする周期関数であることがわかる。振り子の支点に対して静止している観察者の視点で考える。 振り子の運動開始時に紐が重りに作用する張力は、 重りに作用する重力の 振り子の軌道の法線方向 ( 向心方向 ) 成分に −1 をかけたものである。 運動開始時の張力は、 重りに作用する重力の 振り子の軌道の法線方向成分によって相殺されるので、 向心力を形成していないのだ。
重りが 加速 ・ 減速 を周期的に繰り返すのが振り子運動の特徴であるが、 重りの移動速度の大きさが、 振り子の軌道の法線方向( 向心方向 )の加速度の要因となる。 そしてこの法線加速度は 向心力 を生み出す。
鶏が先か卵が先かで言うと、 接線方向は、 力 が先で 加速度 が後、 法線方向は、 速度 が先でその次に 加速度 で最後に 向心力 。
軌道の接線方向 :
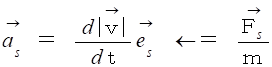
軌道の法線方向( 向心方向 ) :
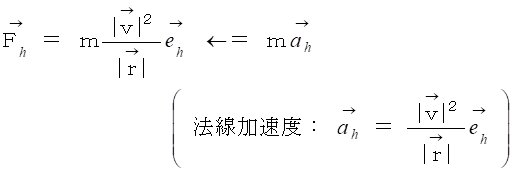
最後に、 重りが 角度
 のときの重りの速さを求めてみよう。 それには、 次の力学的エネルギー保存の法則を表す式を用いる。 重りの最下点の高さを
のときの重りの速さを求めてみよう。 それには、 次の力学的エネルギー保存の法則を表す式を用いる。 重りの最下点の高さを 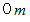 としている。
としている。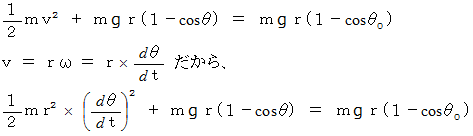

 力学 へ戻る
力学 へ戻る