エネルギーを使用しないにも関わらず、 物質の重力に抗して、 物質の落下速度を遅くしているのは、 空気や水の抵抗です。 それよりもすごいのが、 物質に重力以上の力が働いて、 物質が落下しなかったり、 あるいは逆に上昇したりすることがあります。 その力は、 揚力 または 浮力 です。 代表的なものは、 揚力で浮かぶ飛行機と、 浮力で浮かぶ船です。

　 バックスピンのかかったゴルフボールが高く上がるのは、 揚力の作用によります。 揚力とは、 気流の中で生まれる、 重力に抗して物体の位置エネルギーを上昇させる方向に働く力です。 揚力の原理は、 ２つあります。 それは、 ベルヌーイの定理 と 運動量保存の法則 です。

　 ベルヌーイの定理によりますと、 一連の気流のある所では、 どの点でも、 気圧と運動エネルギー（ 運動エネルギーは、 気流の速さの２乗に比例します。） の和が一定になっています。 したがって、 個体の形状 や 個体の回転などによる気流との摩擦 によって、 気流の一様さが乱れ、 個体の上部の気流が個体の下部の気流よりも速くなると、 個体の上から押さえつけようとする気圧よりも、 個体の下部から持ち上げようとする気圧の方が高くなって、 その圧力差が個体に力を及ぼし、 個体の重力に抗して個体を持ち上げるように作用することになります。

　 運動量保存の法則によりますと、 衝突の前後で、 ２つの物質の運動量のベクトル的和は同じになっています。 したがって、 気流が物質にぶつかって、 トータルとして、 下向きの流れに変化したときは、 その物質の運動は上向きの方向に変化していることになります。

　 バックスピンのかかったゴルフボールが高く上がるのはベルヌーイの定理によるものですが、 飛行機が上昇したり落下しないのは運動量保存の法則によります。（ 若干のベルヌーイの定理は影響しますが。） 飛行機には大気を下降させる力の反作用が作用します。 大気を下降させるのは翼です。 翼の下壁は、 相対的に向かってくる大気に対して斜め上方に乗り越えようとしながら大気を下方に追いやります。 翼の上壁の湾曲は、 流れる空気をまとわりつけること（ コアンダ効果と言われます ） によって大気を斜め下方に押しやります。 飛行機が落ちない理由は、 翼による大気を斜め下方へ追いやる力の反作の力なのです。


　 流体のプールの中では、 流体の深い所ほど流体の圧力が大きくなっています。 これは、 気体よりも液体で顕著です。 液体の中に固体が存在するとき、 個体の上部から押さえつけようとする液圧よりも、 個体の下部から持ち上げようとする液圧の方が強くて、 その圧力差が個体に力を及ぼし、 特にその力が個体の重力に等しいかまたは重力よりも大きいとき、 その力を浮力と言います。

　　　　　　　力 ＝ 圧力 × 面積

　下の図は、 液体のプールの中に直方体の物質が存在しているところの断面図です。

　　　　　　　

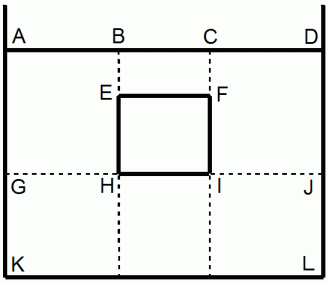
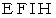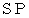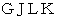　 は、 直方体の断面です。 これから、 わかりやすくするために２次元的に表現していきますが、 実際は３次元のことを言っております。 直方体の上部から押さえつけようとする液圧（ とします ）は、 の範囲に存在する液の質量に重力加速度をかけたものを、 直方体の上部の面積で割ったものです。 また、 直方体の下部から持ち上げようとする液圧（ ＩＰ とします ）は、 ＡＢＨＧ の範囲に存在する液の質量に重力加速度をかけたものを、 ＧＨ の面の面積で割ったものです。 なぜなら、 パスカルの原理 を、 密封された液体 に適応すればいいからです。 パスカルの原理とは、「 密閉容器中の流体は、 ある部分に受けた圧力をそのままの強さで、 流体の他のすべての部分に伝える。」というものです。 したがって、 直方体に働く浮力は次のようになります。

　　　　　　

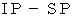　 は、 直方体が液体に置き換わったときの、 その直方体の形をした液体の底にかかる液圧です。 もし、 直方体の密度が液体の密度と等しいならば、 浮力は直方体の重力と等しくなっており、 直方体の密度が液体の密度よりも小さいならば 、浮力は直方体の重力よりも大きくなっています。