【 問 題 】
-
赤玉と白玉をそれぞれ 1/2 の確率で出してくれるガラポン抽選機を使います。1回回せば玉が1個出ます。
エントリーNo.1 さん から エントリーNo.100 さんまでが順番にガラポン抽選機を回します。白玉が出るまで回して出てきた玉はすべて自分の物になります。白玉が出れば次の人と交代します。
(1) 1人がガラポン抽選機を回す回数の平均値はいくらでであると予想しますか?
(2) 全員が終了したときに、全員が持っている赤玉の総数と白玉の総数はおよそ何対何になっていますか?
-
(1) 白玉が初めて出るまでにガラポン抽選機を回す回数の期待値( S )を答えればいいのです。
-
S = 1回×1/2 + 2回×(1/2)2 + 3回×(1/2)3 + 4回×(1/2)4 + ・・・・
これは 等差数列と等比数列の積の和 を求める式です。次のようにして解きます。
(1/2)S = 0回 + 1回×(1/2)2 + 2回×(1/2)3 + 3回×(1/2)4 + ・・・・
S − (1/2)S = 1回 ×{ 1/2 + (1/2)2 + (1/2)3 + (1/2)4 + ・・・・ }
よって、
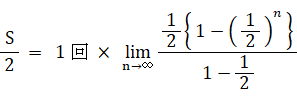
よって、
S = 2回
-
赤玉の総数( T )は次のようになります。
T = ( 0個×1/2 + 1個×(1/2)2 + 2個×(1/2)3 + 3個×(1/2)4 + ・・・・ ) × 100
(1/2)T = ( 0個 + 0個 + 1個×(1/2)3 + 2個×(1/2)4 + ・・・・ ) × 100
T − (1/2)T = 100個 ×{ (1/2)2 + (1/2)3 + (1/2)4 + (1/2)5 + ・・・・ }
よって、
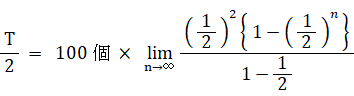
よって、
T = 100個
したがって、 赤玉の総数 : 白玉の総数 = 1:1 です。
-
白玉の総数は 100 個 です。
(1)より、全員が持っている玉の総数は 200 個 と考えられます。
したがって 、赤玉の総数 : 白玉の総数 = 1:1 です。
 確率 へ戻る
確率 へ戻る