私のバイオリンのお師匠さんである親父と10年前から始めた月１回の里帰り２重奏です。 簡単な曲を繰り返しやっています。 独りで弾くときよりもバイオリンがよく鳴ります。 １本の弦の振動がバイオリンの体である箱やその中の空気や異なる弦を共鳴させ、 さらに２台のバイオリンが共鳴し合います。 共鳴をよくするためには、 正確な音程を取ることが大切です。「 理屈っぽいお前のおかげで、 音を弾くことに気を取られ、 曲を弾くことを忘れてしもうた。」 たしかに、 昔の親父のバイオリンには、 うらびれた響きがあり、 どこか懐かしさがありました。

　 両端が固定された弦を指ではじくと、 弦は振動し、 音が聞こえます。 その音の高さは、 次の３つによります。
　　　　弦の線密度（ 単位長さ当たりの質量 ）が小さいほど、 高い音
　　　　弦の張力が大きいほど、 高い音
　　　　弦が短いほど、 高い音

　 このときの弦の振動を視覚的に分析しますと、 それは、 弦の長さの２倍を 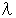としたときに、 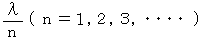の波長の定状波たちが混じったものになっています。 最も波長の長い定状波の波長は弦の長さの２倍です。 定状波とは、 波形が進行せずその場に止まって振動しているように見える波動のことです。 波の節や腹にあたる点の位置が変わらない波動のことです。 定状波は、 波長 ・ 速さ ・ 振幅 が同じで進行方向が互いに逆向きの２つの波が重なり合うことによってできます。 振動する弦の中には、 弦の端から端へと行ったり来たりしながら伝わっている横波たちがいます。 その横波たちは、 自分の波長や振動数と同じ大きさの波長や振動数の定状波を作ります。 また、 その横波たちの弦を伝わる速さは等しくて、 その速さは弦の線密度や張力によって変ってきます。 したがって、 定状波の振動数は次のようになります。

　　　　　より、
　　　　

　 の波長 の定状波というのは、 最も波長の長い定状波（ 波長が 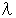の定状波 ）の振動数を 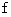としたときに、 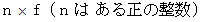の振動数の定状波であると言うこともできます。 なぜならば、 次の式が成り立つからです。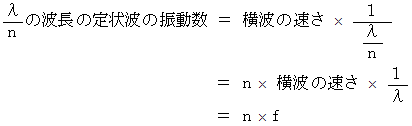
　　　　

　 以上のような弦の振動を、 弦の固有振動と言います。 これが空気を同じ振動数で振動させ、 音となって私たちの耳に聞こえてくるわけですが、 その空気振動たち（ これは、 縦波で音波と言います。）の波長は、 定状波たちの波長とは異なります。 なぜならば、 次の式が成り立っているからです。

　　　　　より、
　　　　

　 弦の固有振動が引き起こす最も振動数の小さな音波の振動数を 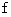とすると、 弦の固有振動は、 無数の 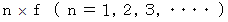の振動数の音波を引き起こしていると言えます。 このような音波の集合を、「 固有振動による倍音の集まり 」と言います。 ヒトの聴覚は、 これについては、 １つの音として聞き、 そのうちの最も振動数の小さな音波の振動数を、 その音の高さであると判断します。 また、倍音の構成比率は音色を決めます。 音の３要素は、 大きさ（ 音波の振幅 ）、 高さ（ 音波の振動数 ）、 音色（ 音波の波形 ）です。

　 弦の線密度と張力を固定したときは、 弦を伝わる横波の速さが一定になりますので、 弦の長さが定状波の振動数を決めることになります。 最も波長の長い定状波の振動数を 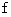とすると、 その弦が発する音の振動数は 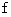になります。 そして、 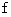は次のように表されます。
　　　　
　 この式から、 弦が発する音の振動数は弦の長さに反比例することがわかります。 また、 音波は、 音速が一定であるため、 振動数は波長に反比例しますので、 弦が発する音の波長は弦の長さに正比例することもわかります。

　 弦の線密度と張力を固定したときは、 弦の振動が発する音の振動数の比の逆数をとったものは、 弦の長さの比になります。
ドレミファソラシド の振動数比は、
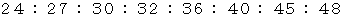　　　　　　　　ですから、
ドレミファソラシド を発する弦たちの長さの比は、 次のようになります。
　　　　
　　　　　　　　　　　　

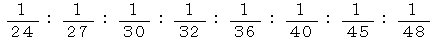
そこで、 次のような、 バイオリンの弦を指で押さえる位置の図を作ることができます。
　　　

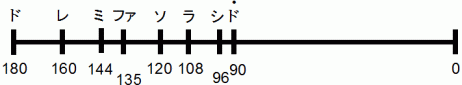
　 バイオリンでニ長調の音階を弾くならば、 ド の音は第３弦の開放弦（ 指を押さえない音 ）で弾き、 レ ミ ファ と順に、 第２指、 第３指、 第４指 で押さえていき、 ソ ラ シ ド は、 ポジションチェンジして、 順に、 第２指、 第３指、 第４指、 第５指 で押さえていきます。 ソ ラ シ ド は、 第２弦に移ってから、 順に、 開放弦、 第２指、 第３指、 第４指 で押さえてもいいです。

　 音階は、 螺旋階段で、 サイクル構造です。 そして、 音は、 振動です。 サイクル運動の典型である、 バネばかりのおもりが上下するような単振動は、 等速円運動する物質の投影です。 等速円運動の前半の半周の投影が単振動の運動範囲になっています。 こう考えてくると、 上図から、 直角が90度になった理由の仮説ができそうです。しかし、 定説の「 古代は、 深夜０時の星の位置が、 北極星を中心とする円を360日で一周すると考えたことに由来する。（ 星たちは、 この年周運動とは別に、 日周運動もしています。）」は説得力がありますので、 この仮説はきっと間違いでしょう。

　 バイオリンの奏法に、 ハーモニックス や フラジオレット というのがあります。 これらは、 指を軽く弦に触れ、 弓にあまり圧力をかけずに弾くことで、 共鳴感のある高い音を出します。
　 弦の長さを 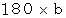とします。
　 手前の駒（ 弦の一端 ）から 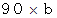の位置に指を触れて弾くと、 １オクターブ高い ド の音が出ます。 この場合は、 指をしっかり押さえた時と同じ高さの音です。
　 手前の駒（ 弦の一端）から 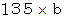または 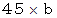の位置に指を触れて弾くと、 ２オクターブ高い ド の音が出ます。 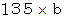の位置をしっかり押さえて普通に弾くと ファ の音であり、 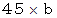の位置をしっかり押さえて普通に弾くと ２オクターブ高い ド の音です。
　 手前の駒 （ 弦の一端 ） から 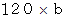または 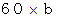の位置に指を触れて弾くと、 １オクターブ高い ソ の音が出ます。 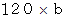の位置をしっかり押さえて普通に弾くと ソ の音であり、 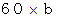の位置をしっかり押さえて普通に弾くと １オクターブ高い ソ の音です。 このフラジオレットをすると、 １つ上の弦が共鳴して振動を始めます。 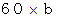の位置のフラジオレットは、 調弦のときに役立ちます。 また、 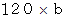の位置のフラジオレットは、 楽器の目覚めが悪い時に使用すると効果があります。 楽器の目覚めとは、 楽器自体がよく共鳴し始めることです。 バイオリンがよく鳴りだしたときには、「 お父さん、 ごはんよ〜。」に対して、 なかなかやめられなくなります。