(1) 半減期が解れば 〇年後の原子数が解る
-
放射性原子は崩壊していきますが、 元の半数になるまでの時間を半減期と言います。
最初の原子数を
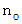 、 半減期を
、 半減期を  とすると、
とすると、  の時間後の原子数
の時間後の原子数  は次の式で表されます。
は次の式で表されます。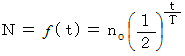
半減期を求めるには、 この式の逆関数を利用します。
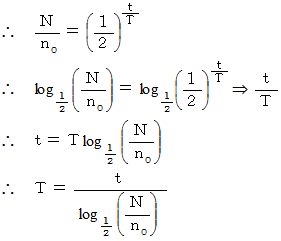
たとえば、 3年後に元の90%になっていたとします。
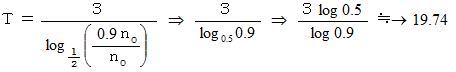
したがって、 半減期が 19.74年 であることが解ります。
では、 半減期が20年の原子は、100年後には何パーセントになっているでしょうか?
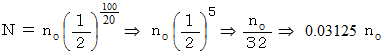
したがって、 約 3.1 %であることが解ります。
-
放射性原子核が崩壊する速さは、 放射性原子核の数に比例しますので、 次の式が成り立ちます。

崩壊定数とは、 単位時間あたりに放射性原子核が崩壊する確率のことです。
崩壊開始時の放射性原子核の数を N0 として、 t 秒後の放射性原子核の数を求めてみましょう。
 より、
より、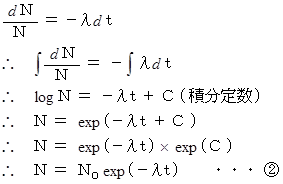
さて、
 に
に を代入して、
を代入して、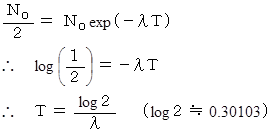
上記の式が、 半減期と崩壊定数の関係式です。
この式は(1)の最初の式からも導くことができます。
 も使って、
も使って、
 基礎物理学 へ戻る
基礎物理学 へ戻る