（１） 無限大 と 無限小 と ゼロ

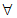全体集合を 以上の実数とします。 無限小を記号 で表すことにします。 すると、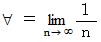
　　　　
　　　　　であり、　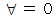　ではない。
　　　　
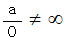　　　　　であり、 そもそも 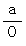という式は禁忌である。
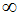　　　　 や 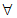は実数ではないので、 全体集合の要素ではない。

（２） 無限小

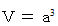　 の体積を持つ立方体の「 体積要素 」の体積 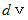は、 次のように表されます。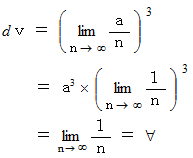
　　　　
また、 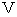と 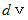の関係は、 次のようになります。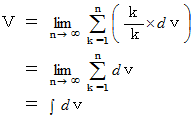
　　　　

（３） 無限遠方垂直平面

　 二次元平面の 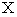軸 と 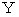軸 は、 無限に伸ばしても原点以外では交わりません。 また、 ２つの平行線は、 無限に伸ばしても交わらないと思うのですが、 無限遠方垂直平面上では、 １点で交わるものと定義する数学的方法もあるそうです。 こう定義すると、 放物線も無限遠方垂直平面上では１点で交わることになるそうです。 このように、 平行線が無限遠方垂直平面上では１点で交わるものと定義しようとするのには理由があります。 それは、 無限に広がる垂直平面が無限遠方に存在する場合は、 点になるとイメージするからです。 ですから、 無限遠方垂直平面とはいわずに、 無限遠点 」 言われます。 私は、 ちょっと無理があるように思います。 限られた範囲の面が、 無限遠方では立体角が になるというのなら納得いくのですが ・ ・ ・ 。

（４） 無限遠垂直平面から来る平行光線について

　 ある点で放たれた光が別の点に届くのは最短コース１つだけです。 しかし、 私たちは点で光を捉えているのではありません。 目はレンズであり、 レンズは面です。 このとき、 一瞬 １ 点から放たれる光は粒子としての光子としてみれば、 無数の光子が四方八方に飛び出していますが、 波として光をみれば、 四方八方にモワ〜ッと広がっていきます。 そして、 光源が無限の遠方にあるときは、 その光源点からみた私たちの目のレンズの面の立体角は ステラジアンになり、 私たちの目のレンズの面に飛び込んでくる、 点から放たれた光子の波の一部は、 広がりを持っていないはずです。 私はこれを、「 受光面にとっての点光源からの平行光線 」と言っています。 これは遠方視や望遠鏡のしくみを理解する上で大切な概念です。 月の表面のある点から放たれる光は広がりを持たない平行光線です。 月の真ん中に視線を合わせている時、 月の真ん中の点からくる平行光線は眼内レンズの面に垂直に入ってきますが、 月の辺縁上のある点からくる平行光線は、 眼内レンズの面には少し斜めに入ってきます。 このとき望遠鏡を月に向かって垂直な方向に１０ｍほど平行移動させても望遠鏡に映る月は移動しません。 地球上の１０ｍからすると、 月は無限の遠方にあると考えてさしつかえないからです。


　 ある点で放たれた光が別の点に届くのは最短コース１つだけですが、 ある面上のいろんな点から放たれる光が、 ある点に届くにはすべてコースが異なります。 しかし、 ある面が無限大に離れている場合は、 受光点からみたその面の立体角は ステラジアンになり、 面上のいろんな点から放たれる多数の光のコースは平行になっています。 私はこれを「 受光点にとっての面光源からの平行光線 」と言っています。 太陽の光は、「 受光点にとっての面光源からの平行光線 」ではありません。 その証拠に、 地球から見る太陽の立体角は ステラジアンではなく、 太陽は点ではなく面に見えます。

　　　　　　　　　　


　 円の中に、 テニスのラケットのガットのような構造をした網を張ります。 円の大きさは太陽の直径と等しく、 網の目の大きさは 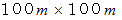とします。 網の結び目（ ガットの交点 ）すべてに光源を付けて光を放ち続けさせます。 観察者の顔の平面に平行になるようにして網円を 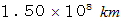離れた所の観察者の正面に置きます。 その次にその網円を光の速さで観察者に衝突するまで移動させます。 そのときに観察者が観察する多くの光源の軌跡（ 光源は見え、 光源の移動の軌跡はイメージに残りますが、 光の伝播の軌跡は見えません。）は、 普通に見る太陽の大きさの塗りつぶされた円の中から放射線状に四方八方に広がる、 仏様の放射光背のように見えます。 もし太陽が無限大の距離離れているのであれば、 放射線を放つ塗りつぶされた円は点になります。この思考実験において、 結び目の光源たちの軌道は、 太陽のいたる部分から放たれる光子たちを象徴しています。 それらはすべて平行な軌道上を飛んできます。 私はこれを「 受光面にとっての面光源からの平行光線 」と言っています。 移動する網円の中の平面すべての部分の軌跡で作られる円柱の、 観察者から見える円の部分の立体角は近づいてくるにつれて大きくなり、 観察者に衝突したときの立体角は 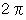になります。 観察者に衝突したときの観察者から見える円の部分の直径は、 太陽の直径と等しくなっています。 このモデルは、 放射線状に広がる 太陽の暈（かさ） や 光芒 などの現象を説明するためのモデルです。 これらの現象は、 本来ならば私たちに届かない光の一部が、 屈折によって私たちに届き、 私たちには本来見えない光の伝播の軌跡たちを見せてくれるのです。 また、 このモデルは、 光の伝播ではないけれども流星群の放射点の説明にも応用できます。