 確率 へ戻る
確率 へ戻る 大学生のための数学 へ戻る
大学生のための数学 へ戻る|
|
容 疑 者 Y の 選 択 |
||
|
自 白 |
黙 秘 |
||
|
容 疑 者 X の 選 択 |
自
白 |
X : 懲役 5か月
Y : 懲役 5か月
|
X : 釈放
Y : 懲役 11か月
|
|
黙
秘 |
X : 懲役 11か月
Y : 釈放
|
X : 釈放
Y : 釈放
|
|
 容疑者X による したたかな計算 :
容疑者X による したたかな計算 : とし、 自分が自白する確率を
とし、 自分が自白する確率を  とするとき、 自分が刑期を含めて拘束される長さの期待値を
とするとき、 自分が刑期を含めて拘束される長さの期待値を とします。 すると、 次の式が成り立ちます。 なお、 自白したとしても取り調べ中の1 か月間は拘束され、 その直後に懲役刑が始まるとします。
とします。 すると、 次の式が成り立ちます。 なお、 自白したとしても取り調べ中の1 か月間は拘束され、 その直後に懲役刑が始まるとします。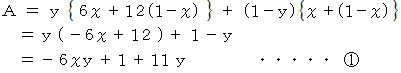
 が
が  から
から  の間のどんな実数をとろうとも、
の間のどんな実数をとろうとも、  が最小になるのは、
が最小になるのは、  から
から  の間の値をとり得る
の間の値をとり得る  が
が  のときです。
のときです。 容疑者Y による したたかな計算 :
容疑者Y による したたかな計算 : とし、 自分が自白する確率を
とし、 自分が自白する確率を  とするとき、 、 自分が刑期を含めて拘束される長さの期待値を
とするとき、 、 自分が刑期を含めて拘束される長さの期待値を とします。 すると、 次の式が成り立ちます。 なお、 自白したとしても取り調べ中の1 か月間は拘束され、 その直後に懲役刑が始まるとします。
とします。 すると、 次の式が成り立ちます。 なお、 自白したとしても取り調べ中の1 か月間は拘束され、 その直後に懲役刑が始まるとします。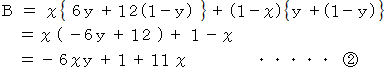
 が
が  から
から  の間のどんな実数をとろうとも、
の間のどんな実数をとろうとも、  が最小になるのは、
が最小になるのは、  から
から  の間の値をとり得る
の間の値をとり得る  が
が  のときです。
のときです。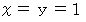 のとき、
のとき、  と
と  より、
より、  になります。
になります。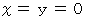 のときは、
のときは、
 と
と  より、
より、 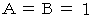 になります。
になります。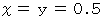 のときは、
のときは、  と
と  より、
より、  になります。
になります。