（１） ミニビンゴゲーム

　 ３ × ３ ＝ ９ 枠で中央枠フリーのミニビンゴゲームは、 あらかじめ １ 〜 24 の自然数の中から異なる数字を選んで好きな枠内に１個ずつ記入しておき、 １ 〜 24 の自然数から１回選んだ数字を除去しながら抽選を繰り返していって、 横の３列または縦の３列または斜めの２列のいずれかの列のすべての数字が抽選され次第「 上がり 」になり、 早く上がる順番を競うものです。 ただし、 次のシュート（ 数字の抽選 ）で上がる可能性が生じた時には「 ビンゴ 」と宣言しなければなりません。 最善の場合は２回のシュートで上がり、 最悪の場合は21回のシュートで上がります。

　 では、 12回のシュートまでに上がる確率を求めてみましょう。 いわゆる12回までの累計確率というやつです。

（ 考え方その１ ）

　 12回シュートすると、 平均すると、 自分が選んでカードに記入していた数字８個のうち４個が抽選されます。
　 抽選された数字たちを赤字で表し、 抽選されなかった数字たちを黒字で表し、 赤字たちの配置により上がりになるための確率を考えます。

　　　　

　　　　

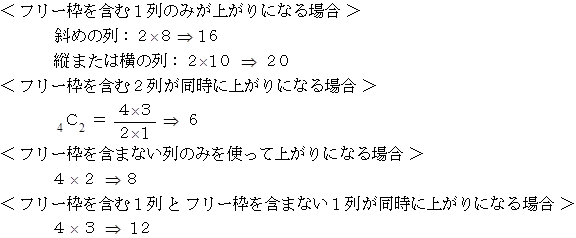
したがって、 赤字たちの配置により上がりになるための確率は次のようになります。

　　　　


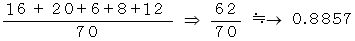
（ 考え方その２ ）

　 すべてのビンゴカードの数の配列の場合の数は 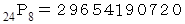です。 実際のビンゴゲームではシュートして数字を選んでいくのは任意なのですが、 随意に １、 ２、 ３、 ・ ・ ・ 　と選んだとしても、 その確率は変わらないことになります。 そこでこの場合について検討してみましょう。 すると、 12回のシュートによって抽選された数字は、 １ 〜 12 までの12個の数字になります。 では、 上がりになっている場合の数をケースごとに見ていきましょう。 「 これまでのシュートで集められた数 」 とは、 １ 〜 12 までのどれかの数です。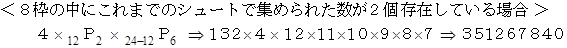










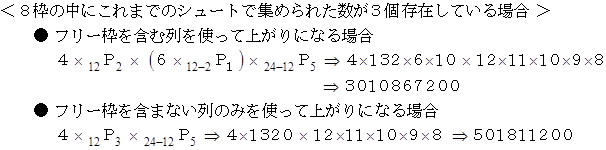
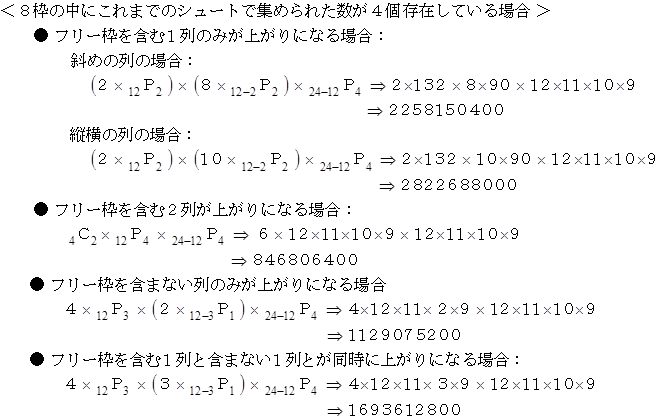
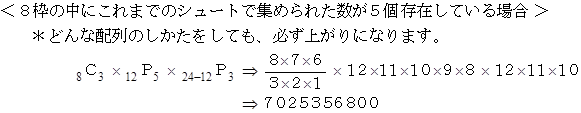
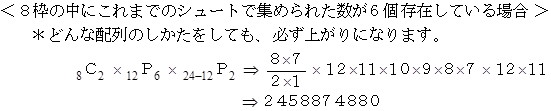
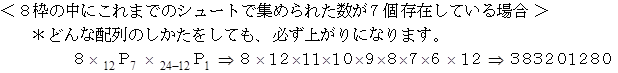
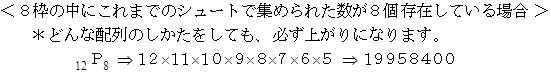
　したがって、 １ 〜 12 の数字たちによって上がりになる確率は次のようになります。

　　　　


（ プログラムによるシミュレーション ）

　 では、 どっちの考え方が正しいのでしょうか？　まず、 シミュレーションプログラムで何回か試してみてください。


　　　

　　　　　　今回は 回目に上がりました。

　 では、 統計をとるために、 次のような十進BASIC のプログラムを組んで、 コンピューターシミュレーションをしてみましょう。


　 すると、 考え方その２ の方が正しいことが解ります。 では、 どうして考え方その１ は間違っているのでしょうか？　12回シュートすると、 平均すると、 自分が選んでカードに記入していた数字８個のうち４個が抽選されることは間違いありません。 また、 ８枠の中に４つの赤字と４つの黒字を配置する場合の数も間違いありません。 また、 ４つの赤字で上りの配置を作る場合の数も間違いありません。 ではいったいどうして？　それは次の理由によります。
　 もし12回シュートしたときに３つの数字が抽選される確率と５つの数字が抽選される確率とが異なること、 ５つの数字が抽選された場合はすべて上りになるのに、 ３つの数字が抽選された場合は上りになる確率は比較的少ないこと。 そういうわけで、 ４つの数字の前後で対称になっていないことが、 その理由なのです。

（２） 一般的なビンゴゲームの方法

　 ５ × ５ ＝ 25 枠で中央枠フリーのビンゴゲームは、 １ 〜 75 の数字から異なる数を24個選んであらかじめ好きな枠内に１個ずつ記入しておき、 １ 〜75 の数字をみんなで順番に任意に選んでいって（ １回選んだ数字は捨てていく ）、 その数字が記入されている枠を塗りつぶしていき、 縦５列または横５列または斜５列のいずれかがすべて塗りつぶされ次第「 上がり 」になり、 早く上がる順番を競うものです。 ただし、 次のシュート（ 数字の抽選 ）で上がる可能性が生じた時に、「 ビンゴ 」と宣言しなければなりません。