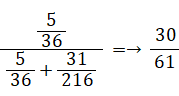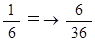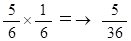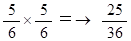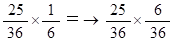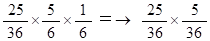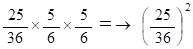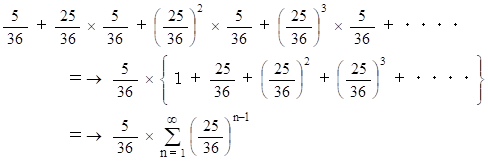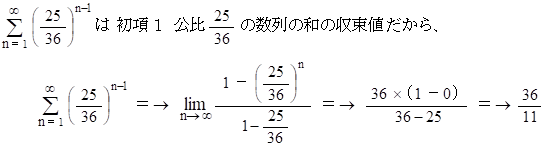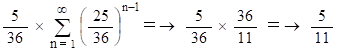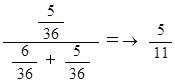交互にチャレンジする念願成就早い者勝ち
 確率 へ戻る
確率 へ戻る
 大学生のための数学 へ戻る
大学生のための数学 へ戻る
2022.11.11____
【 問 題 1 】
交互にチャレンジします。A君から始めます。先にコイントスで表が出た方が勝ちです。
A君が勝つ確率を求めなさい。
【 解 答 】
初めてのチャレンジの直後にA君が勝っている確率: 1/2
初めてのチャレンジの直後にB君が勝っている確率: 1/2 × 1/2 =→ 1/4
2人が初めてのチャレンジをした直後に決着がついてない確率: 1/2 × 1/2 =→ 1/4
n 回目のチャレンジの直後にA君が勝っている確率: (1/4)n−1 × 1/2
n 回目のチャレンジの直後にB君が勝っている確率: (1/4)n−1 × 1/4
2人が n 回目のチャレンジをした直後に決着がついてない確率: (1/4)n
2人が n 回目のチャレンジをしたときに、n の値にかかわらず、A君が勝つ確率は 1/2 で、B君が勝つ確率は 1/4 であるから、このゲームで A君が勝つ確率は次の式で与えられる。
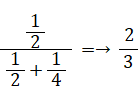
【 問 題 2 】
交互にチャレンジします。A君から始めます。先に各自の念願成就した方が勝ちです。
A君の念願: 2つのサイコロを振ったときに、出た目の数の和が6になる。
B君の念願: 2つのサイコロを振ったときに、出た目の数の和が7になる。
A君が勝つ確率を求めなさい。
【 解 答 】
1回のチャレンジでA君の念願が成就する確率: 5/36 ※(1,5)(2,4)(3,3)(4,2)(5,1)
1回のチャレンジでB君の念願が成就する確率: 6/36 =→ 1/6 ※(1,6)(2,5)(3,4)(4,3)(5,2)(6,1)
初めてのチャレンジの直後にA君が勝っている確率: 5/36
初めてのチャレンジの直後にB君が勝っている確率: 31/36 × 1/6 =→ 31/216
2人が初めてのチャレンジをした直後に決着がついてない確率: 31/36 × 5/6 =→ 155/216
n 回目のチャレンジの直後にA君が勝っている確率: (155/216)n−1 × 5/36
n 回目のチャレンジの直後にB君が勝っている確率: (155/216)n−1 × 31/216
2人が n 回目のチャレンジをした直後に決着がついてない確率: (155/216)n
2人が n 回目のチャレンジをしたときに、 n の値にかかわらず、A君が勝つ確率は 5/36 で、B君が勝つ確率は 31/216 であるから、このゲームで A君が勝つ確率は次の式で与えられる。
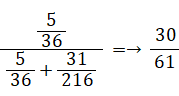
【 問 題 3 】
A君とB君が競います。サイコロを交互に振って先に1が出た方が勝ちです。先手はA君です。このゲームでB君が勝つ確率を求めてください。
【 解 答 】
第1投目に
A君が勝つ確率:
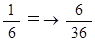
B君が勝つ確率:
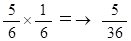
勝負がつかない可能性:
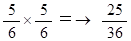
第2投目に
A君が勝つ確率:
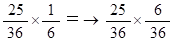
B君が勝つ確率:
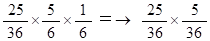
勝負がつかない可能性:
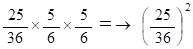
第3投目に
以下(略)
このゲームでB君が勝つ確率:
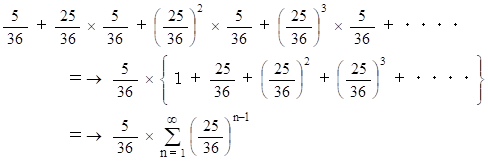
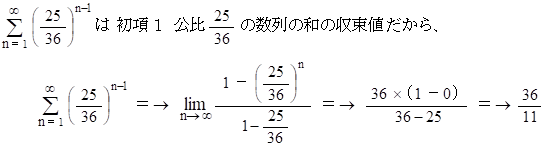
したがって、
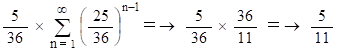
【 別 解 】
第1投目で決着がつかなかった場合は、その時点で、第2投目は第1投目と考えることができます。ということは、第1投目でA君が勝つ確率とB君が勝つ確率を用いて、次のようにして、このゲームでB君が勝つ確率を求めることができます。
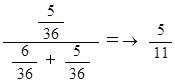
プログラムの内容 :
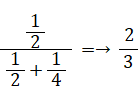
 確率 へ戻る
確率 へ戻る