Ａ君の慣性系 ：
　　　Ａ君の西側にＢ君がいて、Ａ君の東側にＣ君がいる。
　　　Ｂ君とＣ君は同じ角速度で自転している。
　　　Ｂ君とＣ君はＡ君から同じ距離 r_Ａ だけ離れている。
　　　Ｂ君とＣ君はＡ君に向かって同じで一定の速さ v で移動し続けている。
　　　Ｂ君とＣ君はそれから ｔ_Ａ 後に、ちょうど１自転した瞬間にＡ君に衝突した。

Ｂ君の慣性系 その１ ：
　　　Ｂ君の東側にＡ君とＣ君がいる。
　　　Ｂ君とＣ君は同じ角速度で自転している。
　　　Ａ君はＢ君から r_Ｂ だけ離れている。
　　　Ｃ君はＢ君から ２r_Ｂ だけ離れている。
　　　Ａ君はＢ君に向かって一定の速さ v で移動し続けている。
　　　Ｃ君はＢ君に向かって一定の速さ −x で移動し続けている。
　　　Ｂ君とＣ君はそれから ｔ_Ａ 後に、 ちょうど １ 自転した瞬間にＡ君に衝突した。

Ｂ君の慣性系 その２ ：
　　　Ｂ君の東側にＡ君とＣ君がいる。
　　　Ｂ君とＣ君は同じ角速度で自転している。
　　　Ａ君はＢ君から r_Ａ だけ離れている。
　　　Ｃ君はＢ君から ２r_Ａ だけ離れている。
　　　Ａ君はＢ君に向かって一定の速さ v で移動し続けている。
　　　Ｃ君はＢ君に向かって一定の速さ −x で移動し続けている。
　　　Ｂ君とＣ君はそれから ｔ_Ｂ 後に、 ちょうど １ 自転した瞬間にＡ君に衝突した。

合成速度の式よりxを求める ：
　　　Ａ君に対するＢ君の速さ ＝ v　　　（ これはＡ君の慣性系でのこと ）
　　　Ｂ君に対するＣ君の速さ ＝ −２v　（ これはＡ君の慣性系でのこと ）
　　　Ｂ君に対するＣ君の速さ ＝ x　　　（ これはＢ君の慣性系でのこと ）
　　　Ａ君に対するＣ君の速さ ＝ −v　　（ これはＡ君の慣性系でのこと ）
　　　　　　　　　　　（ 光の速さを １ とする単位系を用いる ）
　　　合成速度の式より、
　　　　　　
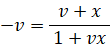
　　　よって、
　　　　　　

Ａ君の慣性系 と Ｂ君の慣性系その１ との比較 ：

距離 ＝ 速さ × 時間　より
　　　
よって、
　　　
　 ｔ_Ａ ＜ ｔ_Ｂ　ということは、 Ｂ君やＣ君が１自転するのに要する時間がＡ君の慣性系よりＢ君の慣性系で多くなっているということなので、 Ｂ君の慣性系ではＡ君の慣性系よりも彼らの自転がゆっくりと行われているということである。 ということは、 Ｂ君の慣性系ではＡ君の慣性系よりも時間の経過しているスピードがスローであるということである。 というわけで、「 移動している慣性系の時間は短縮している。」

Ａ君の慣性系 と Ｂ君の慣性系その２ との比較 ：

時間 ＝ 距離 ÷ 速さ　より
　　　
よって、
　　　
　 r_Ａ ＞ r_Ｂ　ということは、 Ｂ君やＣ君が１自転する間に移動するＣ君の距離がＢ君の慣性系の方がＡ君の慣性系よりも距離が短くなっているということである。 というわけで、「 移動している慣性系の空間は短縮している。」