【 問 題 １ 】

y ＝ x^２　（ ０ ≦ x ） のグラフの 直線　y ＝ x　に対する鏡像の曲線の方程式を求めよ。

【 解 答 】

Ｘ ＝ y ＝→ x^２
Ｙ ＝ x
よって、
　　　
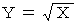
したがって答えは、
　　　

【 問 題 ２ 】

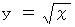
　 y ＝ x^２　（ ０ ≦ x ）　のグラフを、 x 軸方向に３倍　y 軸方向に２倍　拡張した後、 x 軸方向に２　y 軸方向に３　平行移動した。 その曲線を表す方程式を求めよ。

【 解 答 】

Ｘ ＝ ３x
Ｙ ＝ ２y ＝→ ２x^２
よって、
　　　
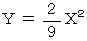
Ｘ’ ＝ Ｘ ＋ ２

よって、
　　　
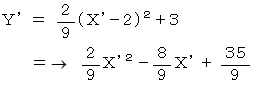
したがって答えは、
　　　

【 まとめ 】

　　　　　

　 グラフの写像は、 基本的には点の写像です。 写像を受ける点がグラフ上の点だけであるというところが、 一般の写像と異なるところです。