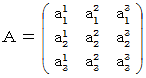
上の３次正方行列の逆行列は、 次のように表されます。
　　　　


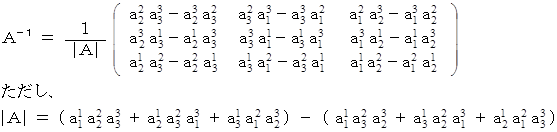
（１） 逆行列を求めることによって連立３元一次方程式を解く

　
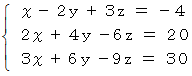
　 上のれ連立３元一次方程式の解は 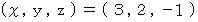　です。 これを求めるのに逆行列を用いる方法があります。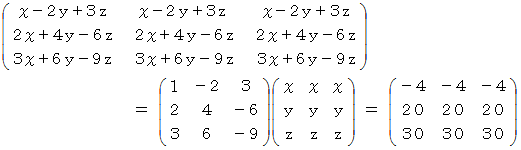
　　　　
　　　　
　　　　
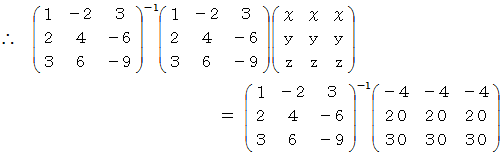
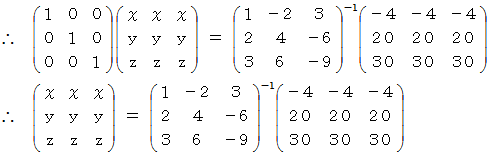
ここで、
　　　　
　 これは困ったことになりました。 そうです。 必ずしも連立３元一次方程式の解は行列を用いて解くことができるとは限らないのです。 では、 次のケースはどうでしょうか？
　
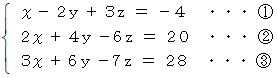
　 上の連立３元一次方程式の解は 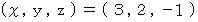　です。 逆行列を用いて求めてみましょう。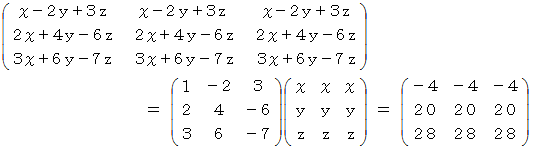
　　　　
　　　　
　　　　
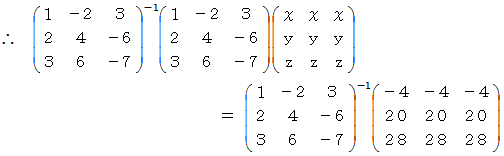
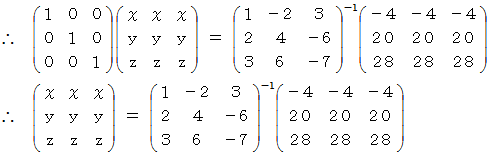
ここで、
　　　　
　　　　
　　　　

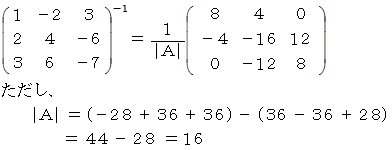
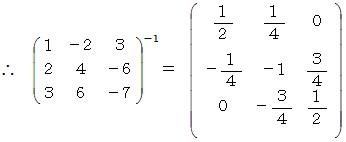
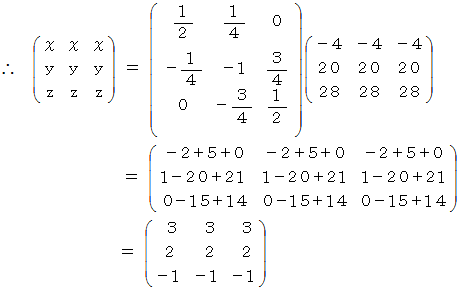
　 今度はうまくいきました。 普通にこの連立３元一次方程式を解くときは、 まず の両辺を２倍したものと を辺々加えて の値を求め、 次に下の連立２元一次方程式を解くといいでしょう。 逆行列を用いるよりも普通に解く方が簡単です。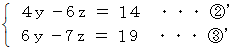
　
　 逆行列を簡単に求めることのできるパソコン用アプリケーションソフトがあるときには、 多元１次連立方程式の解を求めるときに行列を用いると簡単にいく場合があります。


＜ ３×３行列の逆行列を求める ＞
　　　　X(0,0)　X(0,1)　X(0,2)　　　　1/5　　2　　3
　　　　X(1,0)　X(1,1)　X(1,2)　　　　　4　　5　　6
　　　　X(2,0)　X(2,1)　X(2,2)　　　　　7　　8　　9
　　　　　　　上記の行列の入力方法 ：　1/5,2,3,4,5,6,7,8,9

行列 ：　

　　



　　　プログラムの内容

（２） 連立３元一次方程式を解くことによって逆行列を求める

　　　
　　　
　　　
これは、次の３つの式に分解されます。
　　　
　　　
　　　

　 以上の３つの行列を、 それぞれ連立３元一次方程式を解くことによって、 χ₁ 〜 ｚ₃ の値を求めることができます。 すると逆行列が解ります。 では、 この方法で次の行列の逆行列を求めてみましょう。
　　　　　

　
から を辺々引いて、
　　　
と を辺々足して、
　　　
と を に代入して、
　　　
したがって、
　　　
同様にして
　　　
したがって、
　　　

（３） 余因子行列から逆行列を求める

例として、 次の行列の逆行列を求めてみましょう。
　　　　


　　　　
　　　　　　　
上記の方法で行列式を求める方法を、 余因子展開と言います。


　　　　　　　

の 行 と 列 を入れ替えて
　　　　
　 この行列は、 行列Ａの余因子行列と言われます。 余因子行列 と 行列式 と 逆行列 には、 次のような関係があります。
　　　　
したがって、
　　　　
確かめてみましょう。
　　　　

※ 参照： 線形代数学 ＞ 掃き出し法で逆行列を求める