（ 問 題 ）

　 １万人の成人を対象に調査したところ、 運転免許を持っている人が平均して週１回以上カレーライスを食べている割合は 12% で、 平均して週１回以上カレーライスを食べている人が運転免許を持っている割合は 92% でした。 運転免許を持っていて、 かつ、 週１回以上カレーライスを食べている人は、 およそ何人だったのでしょうか？　また、 運転免許を持たず、 かつ、 平均して週１回未満しかカレーライスを食べていない人は、 およそ何人だったのでしょうか？

（ 解 答 ）

　 運転免許を持っていて、 かつ、 週１回以上カレーライスを食べている人は、 およそ 1100人 です。
　 運転免許を持たず、 かつ、 平均して週１回未満しかカレーライスを食べていない人は、　およそ 700人 です。

　「 運転免許を持っているかどうか 」と「 平均して週１回以上カレーライスを食べているかどうか 」とは互いに完全に独立な事象に近いものであることは明白です。 ですから、 全体でも、 週１回以上カレーライスを食べている人の割合は 12% で、 運転免許を持っている人の割合は 92% です。
　 運転免許を持っていて、 かつ、 週１回以上カレーライスを食べている人の数は、 次の式から導くことができます。
　　　　　
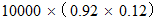
　 運転免許を持たず、 かつ、 平均して週１回未満しかカレーライスを食べていない人の数は、　次の式から導くことができます。
　　　　　

（ 解 説 ）

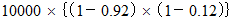
集合Ａ に含まれる確率を ａ 、 集合Ｂ に含まれる確率を ｂ とします。
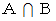に含まれる確率は 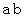になります。 これは「 確率の直列つなぎ 」と言えます。
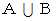に含まれる確率は 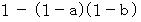になります。 これは「 確率の並列つなぎ 」と言えます。

　 さて、 陥りやすい間違いとして、 ２つの事象が互いに完全に独立ではないのに、「 確率の配列 」を行ってしまうことが多々あります。 たとえば次のような問題があります。

　 　　　あるクラスでは、 ４分の１がマンション以外の住居に住んでいる。
　 　　　また、 ３分の１ が犬を飼っている。
　 　　　また、 マンションに住んでいて犬を飼っていない生徒は 14人 である。
　 　　　では、 マンション以外の住居に住んでいて犬を飼っている生徒は何人か？

　 この２つの事象は互いに完全に独立ではありません。 マンション以外の住居に住んでいる人はマンションに住んでいる人よりも犬を飼う傾向にあるという事実があるのです。
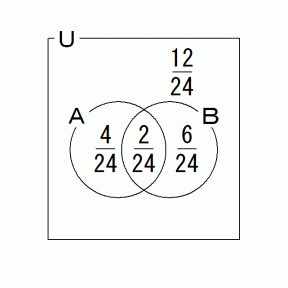
　 ここの所を勘違いすると、 この問題が解けなくなります。 答えは、 次のベン図が示すように４人なのですが ・ ・ ・ ・ 。
　　　　　
　　　　　　　　　　　　　集合Ａ ：　マンション以外の住居に住んでいる生徒
　　　　　　　　　　　　　集合Ｂ ：　犬を飼っている生徒

　 もし、 次のような３つの誤解をした場合、
　マンション以外の住居に住んでいて犬を飼っている生徒は、 全体の 12分の１ である。
　マンション以外の住居に住んでいる生徒が犬を飼っている確率は、 ３分の１ である。
　犬を飼っている生徒がマンション以外の住居に住んでいる確率は、 ４分の１ である。
　「 犬を飼ってなくてマンションに住んでいる生徒は１２人ではないか、 設問が間違っているのではないか。」 いう疑惑にかられるのではないでしょうか。
　　　　　

　 ちなみに２つの事象が互いに独立であるかどうかを検定する方法には、 カイ２乗検定などがあります。 独立検定では、 総数が少ないと互いに関係性があると診断しづらくなる性質があります。

　 ２つの事象の関係性が 0 〜 100 ％ の間を自由に取るものとして、 ４分の１ の確率事象 と ３分の１ の確率事象の絡み合いの模様を 十進BASIC のプラグラムを用いて探ってみました。