力学 へ戻る（ 問 題 ）
-
質量 0.1 kg の球 と 壁がある。
この球と壁の間の反射係数を測定したところ 0.7 であった。
この球を 20 m / s の速さで等速直線運動させ、 この壁に垂直にぶつけたとき、
球が壁に及ぼす（ 壁が球に及ぼす ）力積の大きさを求めよ。
（ 解 答 ）
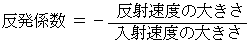※ ただし、 速さの大きさに ＋ や − の符号を与える。以上の式より
跳ね返った球の速さは、 20 × 0.7 ＝ 14 （ m / s ）
力積 ＝ 運動量の変化
＝ 0.1 × （ −14 ） − 0.1 × 20
＝→ −3.4
したがって、 力積の大きさは 3.4（ N s ） である。
力積 ＝ 運動量の変化 ＝ 質量 × 入射速度の大きさ − 質量 × 反射速度の大きさ
＝ 質量 × 入射速度の大きさ ＋ 質量 × 反発係数 × 入射速度の大きさ
＝ 質量 × 入射速度の大きさ ×（１＋反発係数 ）
※ ただし、 速さの大きさに ＋ や − の向きを与える。
質量 8 kg 反発係数 0.5 として、入射速度の大きさを １、２，３，・・・ と増やしていくと、
| 入射速度の大きさ（m/s） | |||||
| 力積（Ns） | |||||
| 反射運動エネルギー（J） |
この表より、力積（ Impulse ）は入射速度の大きさに比例し、反射運動エネルギーは入射速度の大きさの２乗に比例することが分かりました。「インパクトの威力は速さの２倍に比例する。」と言われるのはこのことを示しています。それは、運動エネルギーが速度の大きさの２乗に比例することからしても当然のことだと思われます。ただし、打撃のインパクトの威力はこれだけではなく、打撃の威力を大きくするためには、力積が作用している間に力を作用させることが必要です。このことは「加速しながらボールを捉えよ。」という言葉で表されます。さらに、衝突の威力を考えるときに「 クッション作用 」も考慮に入れなければなりません。ボールをキャッチするときに進展した腕を屈曲しながらキャッチすると手に感じる痛みは軽減されます。それは衝突の威力が軽減されていることに他なりません。どうも、衝突の威力の大きさは運動エネルギーだけでは計測できないようです。衝突の威力を評価する衝突後の現象には、反射運動エネルギー や 衝突時に発生する熱や音のエネルギー や 剛体の変形 などがあります。 ※ 参考： 力学 ＞ 衝撃の程度を表す衝突重量力