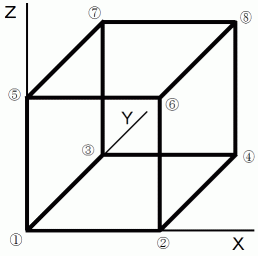
上の図は
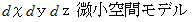 です。
です。 、
、  、
、 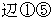 の長さを
の長さを 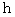 とし、
とし、  をそれぞれ起点とするベクトルを次のように表します。
をそれぞれ起点とするベクトルを次のように表します。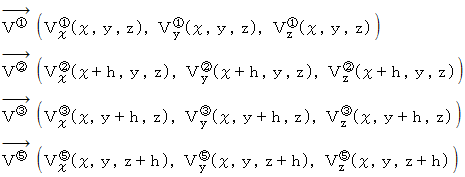
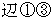 の長さを
の長さを 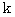 とします。 すると、
とします。 すると、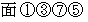 を貫く流れは、
を貫く流れは、 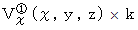 で表されます。
で表されます。 を貫く流れは、
を貫く流れは、 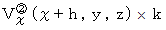 で表されます。
で表されます。 を貫く流れと
を貫く流れと  との差をとり、
との差をとり、 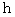 を限りなく小さくすると次のようになります。
を限りなく小さくすると次のようになります。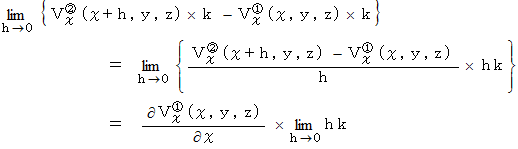
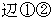 の長さを
の長さを 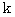 とします。 すると、
とします。 すると、 を貫く流れは、
を貫く流れは、 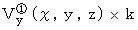 で表されます。
で表されます。 を貫く流れは、 SUB>
を貫く流れは、 SUB>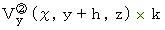 で表されます。
で表されます。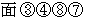 を貫く流れと
を貫く流れと 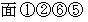 との差をとり、
との差をとり、 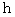 を限りなく小さくすると、 次のようになります。
を限りなく小さくすると、 次のようになります。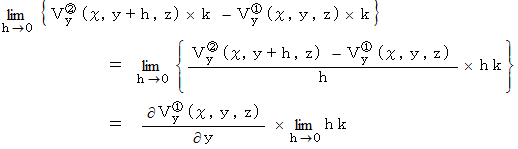
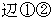 の長さを
の長さを 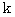 とします。 すると、
とします。 すると、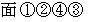 を貫く流れは、
を貫く流れは、 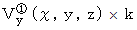 で表されます。
で表されます。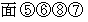 を貫く流れは、
を貫く流れは、 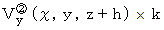 で表されます。
で表されます。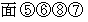 を貫く流れと
を貫く流れと 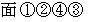 を貫く流れとの差をとり、
を貫く流れとの差をとり、 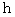 を限りなく小さくすると、 次のようになります。
を限りなく小さくすると、 次のようになります。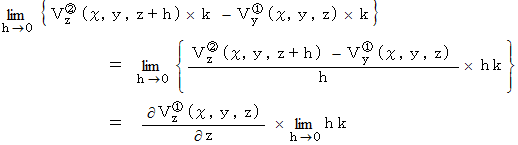
以上の3つの合計をとると、 次のようになります。
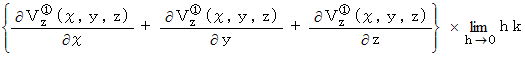
これは、
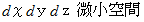 の中で発生した( 湧き出した )流れの量を表しています。 したがって、 次のスカラー量でもって、 微小空間内での湧き出し量と定義し、 これを「 発散 」と言うことにします。
の中で発生した( 湧き出した )流れの量を表しています。 したがって、 次のスカラー量でもって、 微小空間内での湧き出し量と定義し、 これを「 発散 」と言うことにします。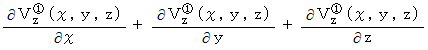
 ベクトル解析 へ戻る
ベクトル解析 へ戻る