２つの正規分布の平均が等しいかどうかの検定をするには、 二標本 ｔ 検定 を用います。 ただし、 この検定は２つの正規分布の分散が等しいことが前提になっていますので、 前もって Ｆ 検定 をして、 そのことを確かめておく必要があります。

　 Ｆ 検定 とは、 ２つの標本分散の比（１以下とする）の二乗が２つの標本数からなる自由度のときの Ｆ分布表（ ｐ＝ 0.05 ） の数値よりも小さければ、 ２つの正規分布の分散が等しいとするものです。

　 二標本 ｔ 検定 は、 ２つの標本から次の ｔ 値 を求めて、
　　　

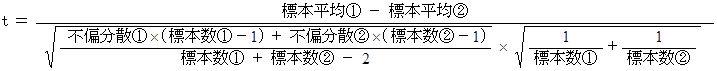
　 自由度 のときの ｔ 分布表（ ｐ＝ 0.05 ）の数値よりも小さければ、 ２つの分散の等しい正規分布は、 平均も等しくて、 これらはまったく同じものであるとするものです。


（ 例題 １ ）

　 ２つの正規分布をなす母集団Ａ と Ｂ は、 標準偏差は不明だが等しいことは解っている。 したがって、 もし、 この２つの平均値が等しいならば、 この２つの母集団は全く同じ正規分布をしていることになる。 そこで２つの母集団から標本を抽出して調査してみた。

　　　母集団Ａ からのサンプリングの結果 ：
　　　　　　7.4　　7.7　　7.3　　7.7　　7.8　　7.6　　7.3　　6.8　　6.9　　7.3　　7.6　　7.2
　　　　　　　　　　　　　　（ 以上 12個のサンプルで、 平均値 7.38　不偏分散 0.10 ）

　　　母集団Ｂ からのサンプリングの結果 ：
　　　　　　6.9　　7.0　　6.7　　7.1　　7.0　　6.9　　7.5　　7.6　　7.4　　6.9
　　　　　　　　　　　　　　（ 以上 10個のサンプルで、 平均値 7.10　不偏分散 0.0889 ）

有意水準 5% で、 この２つの母集団の平均値が等しいといえるか？

（ 解答 ）

　帰無仮説 ：　２つの母集団の平均値は等しい。

　二標本 ｔ 検定の公式に具体的な数値を当てはめると、 次のようになる。
　　　　　

　自由度２０の ｔ 分布表より、 有意水準 5% で 2.086 である。
　2.12＞ 2.086 なので、 帰無仮説は棄却される。
　したがって、 ２つ母平均値は等しくないと言える。


　　　　　　　　＊　「 母集団の分散（ 標準偏差 ）が不明なときは ｔ 分布を用いる。」
　 　　　　　　　　と覚えておくと便利です。

（ 例題 ２ ）

　 全国模擬試験の結果は正規分布に従います。 ある学校のＡ組 （ 生徒数30人 ） の平均点は75点、 標準偏差は5点、 Ｂ組 （ 生徒数32人 ） の平均点は70点、 標準偏差は8点でした。 全国模擬試験の結果からして、 危険率５％の条件下で、 Ａ組とＢ組の学力に差があると言えるでしょうか。

（ 解答 ）

　帰無仮説 ：　Ａ組とＢ組の学力に差はない。
　　　　　　　　　（ それぞれの標本から推測できる全国模擬試験の平均値に有意な差はない。）

　　　　
　　　　

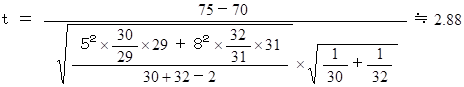
自由度60の ｔ 分布表より、 有意水準 5% で 2.00 である。
2.88　＞　2.00　より、 帰無仮説は否定される。
したがって、 有意水準 5% の条件下で、 Ａ組はＢ組よりも学力が高いと断言できる。