図形の方程式 へ戻る中心が x y 座標系の原点Ｏにあり半径が２の円の方程式は x2 + y2 = 4 です。
この円を平行移動させます。x 軸方向に３、y 軸方向に２。
すると、 この円の方程式は ( x−3 )2 + ( y−2 )2 = 4 となります。
どうして ( x＋3 )2 + ( y＋2 )2 = 4 ではないのでしょうか？
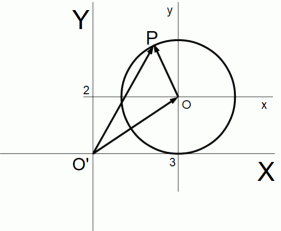
平行移動をさせた後の円の方程式は、 平行移動をさせる前の円を、 x 軸方向に−３、y 軸方向に−２平行移動させた座標系 ( XY 座標系とします ) における円の方程式に等しくなっています。
XY 座標系における x y 座標系の原点Ｏの位置ベクトルは次のように表されます。
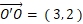
点Ｐの x y 座標系の位置ベクトルを
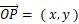とし、点Ｐの XY 座標系の位置ベクトルを
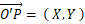とすると、次の式が成り立ちます。
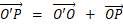
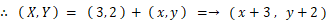
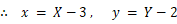
これらを x2 + y2 = 4 に代入して、
( X−3 )2 + ( Y−2 )2 = 4
