ベクトル解析 へ戻る（１） 法線ベクトル と 平面上の １ 点が与えられているとき
-
点Ｑ （
， 
， 
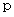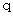） を通りベクトル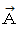 
（ 
， 
， 
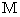） と直交する平面上の点Ｐ （ 
， 
， 
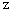） について言えば、次のようになります。
この式が、 点Ｑ を含みベクトル
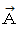と直交する平面の方程式です。 
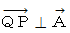なので内積が０であることを示しただけの式なのですが、これが平面の方程式なのです。さて、 たとえば、
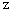＝ ＋３－３ で表わされる平面がどんな平面なのかをイメージしてみましょう。まず、 この平面に垂直なベクトルを求めましょう。 この平面は 点（ １，１，１ ） を含みますので、 次のように置いてみます。
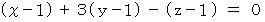
この式を変形すると、
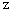＝ ＋３－３ になりますので整合性があります。 したがって、 この平面は ベクトル（ １，３，－１ ） に垂直であることがわかります。 じゃあ、 このベクトルがどんな傾きをもっているかイメージしてみましょう。 平面 と このベクトル の交わる角度を求めてみます。 平面 と このベクトル の交わる角度は、 このベクトル と ベクトル（ １，３，０ ） とのなす角度に等しくて、 それは、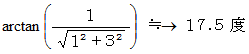 
です。 この平面はこのベクトルに垂直ですから、 この平面は 平面 と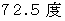 
の角度で交わるということです。この平面は 点（ ０，１，０ ）と 点（ ３，０，０ ）を含みますので、 直線
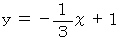上で 平面と交わります。 また、 この平面は 点（ ０，０，－３ ）を含みますので、 原点はこの平面よりも上方にあることもわかります。 これで、 だいたい この平面 がイメージできたと思います。-
次の３点を含む平面のベクトル方程式
Ａ（ ａχ，ａｙ，ａｚ ）， Ｂ（ ｂχ，ｂｙ，ｂｚ ）， Ｃ（ ｃχ，ｃｙ，ｃｚ ）
求める平面上の点Ｐの位置ベクトルを
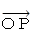とすると、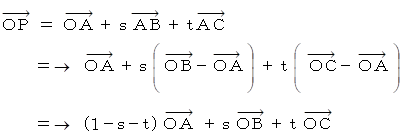
-
空間の３点を含む平面は１つだけです。
A ( 1，2，3 )、B ( 1，－1，1 )、C ( 3，1，2 ) を含む平面の方程式を（１）の方法で求めてみましょう。
求める平面上の点を P ( x，y ) とする。
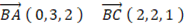
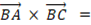
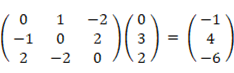
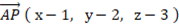
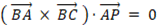より、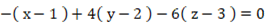
よって、
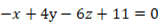
よって、
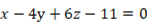
別の解法としては、連立方程式を解く方法があります。 平面の方程式を ax ＋ by ＋ cz ＋ d ＝ 0 とすると、次の３つの方程式が成り立ちます。
a ＋ 2b ＋ 3c ＋ d ＝ 0 ・・・・ ①
a － b ＋ c ＋ d ＝ 0 ・・・・ ②
3a ＋ b ＋ 2c ＋ d ＝ 0 ・・・・ ③
②と③を辺々足して、
4a ＋ 3c ＋ 2d ＝ 0 ・・・・ ④
よって、
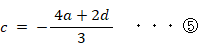
④から①を辺々引いて、
3a － 2b ＋ d ＝ 0
よって、
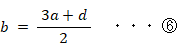
⑤と⑥を②に代入してから両辺に 6 を掛けて、
6a － 9a － 3d － 8a － 4d ＋ 6d ＝ 0
よって、
d ＝ －11a ・・・・ ⑦
⑦を⑤に代入して、
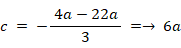
⑦を⑥に代入して、
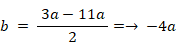
したがって、求める平面の方程式は次のようになる。
x － 4y ＋ 6z － 11 ＝ 0