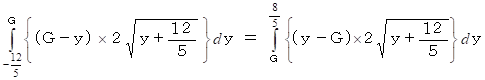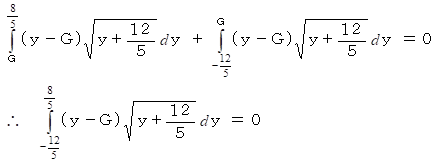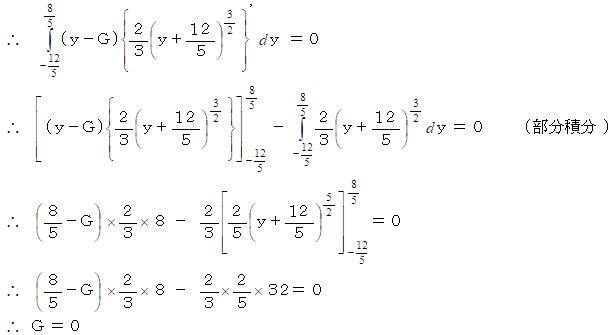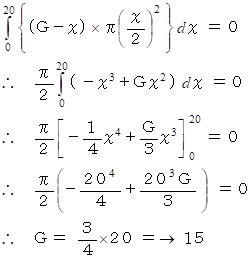平面図の重心とは何か?
 解析学 へ戻る
解析学 へ戻る
 大学生のための数学 へ戻る
大学生のための数学 へ戻る
2017.07.25_____
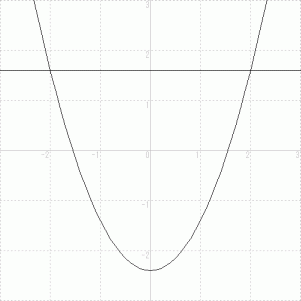
( 問 題 )
( 解 答 )
この図形の最左点は 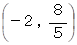 で 最右点は
で 最右点は 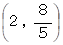 である。
である。
この図形は y 軸に対して左右対称なので、 重心を ( 0,G ) と置くと、 次の式が成り立つ。
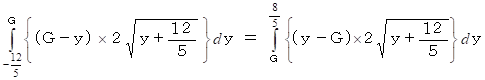
この式は、 x 軸に平行な図形内の線分の長さにその線分の重心線 ( y = G ) からの距離をかけたものを積分したものが、 重心線を中心にして等しいということを表しています。 y 軸に平行な重心線についても同様なことが言え、 2つの重心線の交点が重心になります。
上の式より、
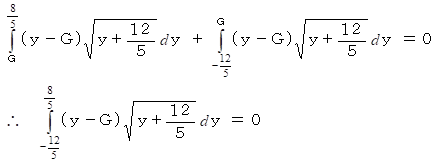
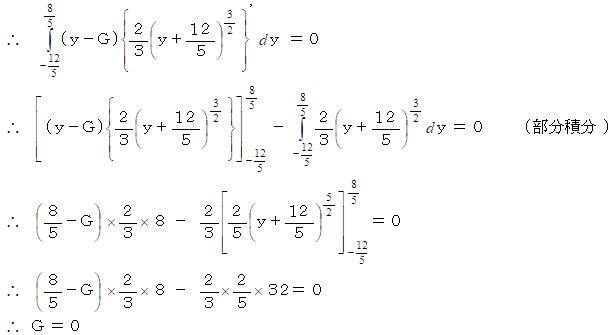
というわけで、 この図形の重心は原点にあることが判りました。
立体の重心も同様の考え方になります。 重心面で切断したときの2つの部分について、 重心面に平行な立体の部分断面積に重心面からの距離をかけたものを積分したものが等しくなっています。 そして1つの直線で交わらない3つの重心面が求められれば、 その交点が重心になります。
たとえば、 底面の半径が 10cm で 高さが 20cm の円錐の重心の底面からの高さを求めてみましょう。
この円錐は y = 1/2・x ( 0 ≦ x ≦ 20 ) を y 軸中心に回転して得られる回転体です。 この回転体の重心の位置を ( G , 0 ) とします。 すると、次の式が成り立ちます。
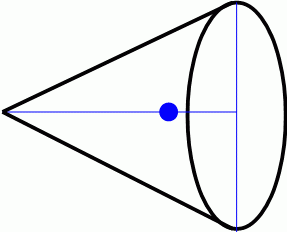
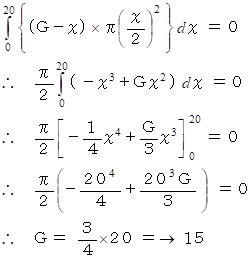
というわけで、 重心は底面から高さ 5cm の所にあることが判りました。
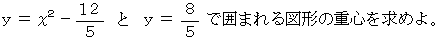
 解析学 へ戻る
解析学 へ戻る 大学生のための数学 へ戻る
大学生のための数学 へ戻る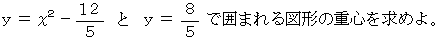

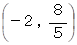 で 最右点は
で 最右点は 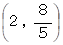 である。
である。