(1) 平面図形の重心線
-
平面図形を平行な線分の集合体であると捉えます。
例えば
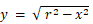 という曲線とX軸 ( y = 0 ) とで囲まれる半円は、 -r ≦ x ≦ r の範囲で 縦×横 =
という曲線とX軸 ( y = 0 ) とで囲まれる半円は、 -r ≦ x ≦ r の範囲で 縦×横 = 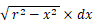 の極細長方形をY軸に平行に敷き詰めたものとして捉えます。 また、この半円は、0 ≦ y ≦ r の範囲で 縦×横 =
の極細長方形をY軸に平行に敷き詰めたものとして捉えます。 また、この半円は、0 ≦ y ≦ r の範囲で 縦×横 = 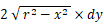 の極細長方形をX軸に平行に敷き詰めたものとして捉えることもできます。
の極細長方形をX軸に平行に敷き詰めたものとして捉えることもできます。敷き詰めた極細長方形のうちの一つが重心線になっています。 そして2つの重心線の交点は重心になります。
-
まず、どこでもいいですから、平面図形と重なってもいいですから、敷き詰められた極細長方形に平行な直線を一つ引きます。それを基準線ということにします。
次に、敷き詰められた極細長方形の面積に基準線からの距離をかけたもの ( 基準線からの方向が逆になるものはマイナスの距離になります ) を 平面図形全体にわたって積分します。いわば、極細長方形の面積の加重総和 ( 基準線から遠いほど重くなる ) を取るのです。すると次のような式が成り立ちます。
極細長方形の面積の加重総和 = 重心線の基準線からの距離 × 平面図形の面積 ・ ・ ・ ①
この式より、重心線の基準線からの距離 が分かります。
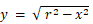 という曲線とX軸( y = 0 ) とで囲まれる半円の重心を求める
という曲線とX軸( y = 0 ) とで囲まれる半円の重心を求める-
この半円の面積は
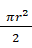 です。
です。この半円を -r ≦ x ≦ r の範囲で 縦×横 =
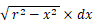 の極細長方形をY軸に平行に敷き詰めたものとして捉えます。
の極細長方形をY軸に平行に敷き詰めたものとして捉えます。Y軸 ( x = 0 )を基準線にします。 平面図形を対称的に2等分する直線は重心線になります。
極細長方形の面積の加重総和を求めます。
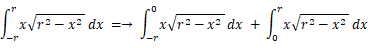
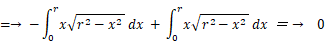
したがって、極細長方形の面積の加重総和 = 0 であることが分かります。
すると、 式 ① より、 重心線の基準線からの距離 = 0 であることが分かります。
というわけで、 重心線の一つはY軸であることが分かりました。
次に、この半円を 0 ≦ y ≦ r の範囲で 縦×横 =
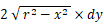 の極細長方形をX軸に平行に敷き詰めたものとして捉えます。
の極細長方形をX軸に平行に敷き詰めたものとして捉えます。Y軸 ( x = 0 )を基準線にします。
極細長方形の面積の加重総和を求めます。
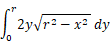
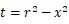 と置くと、
と置くと、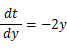 よって、
よって、 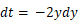
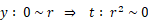
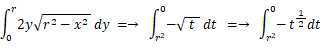
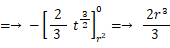
式 ① より、 重心線の基準線からの距離を求めます。
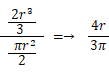
したがって、重心線の方程式は次のようになります。
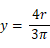
2つの重心線の交点を求め、 それが重心になります。
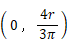
 解析学 へ戻る
解析学 へ戻る