(1) 空間内の曲線を表す 2変数 > 1変数 の 2階層合成関数
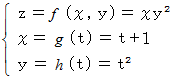
変数
 は、 時間経過と共に連続的に変化するイメージです。そうして、 永遠の過去から永遠の未来へと時が瞬間的に経過したときの
は、 時間経過と共に連続的に変化するイメージです。そうして、 永遠の過去から永遠の未来へと時が瞬間的に経過したときの 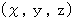 の軌跡がこの曲線を表します。
の軌跡がこの曲線を表します。この曲線の接線ベクトルは、 次のようになります。
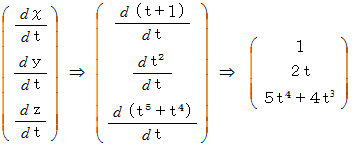
この曲線の

 平面への正投影は、
平面への正投影は、 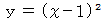 という曲線です。
という曲線です。
 平面へ正投影された曲線の道のりを横軸にとり、 それに対応する空間内の曲線の
平面へ正投影された曲線の道のりを横軸にとり、 それに対応する空間内の曲線の 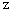 座標値を縦軸にとると、 平面内に曲線ができます。 その曲線の傾きは、 次の2通りの方法で求めることができます。
座標値を縦軸にとると、 平面内に曲線ができます。 その曲線の傾きは、 次の2通りの方法で求めることができます。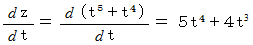

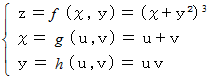
変数
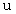 は、 変数
は、 変数  が一定のときに、 時の経過と共に連続的に変化するイメージです。 そうして、 永遠の過去から永遠の未来へと瞬間的に時が経過したら、 今度は、 変数
が一定のときに、 時の経過と共に連続的に変化するイメージです。 そうして、 永遠の過去から永遠の未来へと瞬間的に時が経過したら、 今度は、 変数  が微小に変化して固定し、 変数
が微小に変化して固定し、 変数 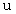 が連続的に変化して、 永遠の過去から永遠の未来へと瞬間的に時が経過し、 ・ ・ ・ ・ と繰り返すと共に、 パラレルワールドにおいては、 変数
が連続的に変化して、 永遠の過去から永遠の未来へと瞬間的に時が経過し、 ・ ・ ・ ・ と繰り返すと共に、 パラレルワールドにおいては、 変数  は、 変数
は、 変数 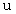 が一定のときに、 時の経過と共に連続的に変化します。 そうして、 永遠の過去から永遠の未来へと瞬間的に時が経過したら、 今度は、 変数
が一定のときに、 時の経過と共に連続的に変化します。 そうして、 永遠の過去から永遠の未来へと瞬間的に時が経過したら、 今度は、 変数 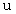 が微小に変化して固定し、 変数
が微小に変化して固定し、 変数  が連続的に変化して、 永遠の過去から永遠の未来へと瞬間的に時が経過し、 ・ ・ ・ ・ と繰り返していって、 幾重にも時が瞬間的に経過したときの
が連続的に変化して、 永遠の過去から永遠の未来へと瞬間的に時が経過し、 ・ ・ ・ ・ と繰り返していって、 幾重にも時が瞬間的に経過したときの 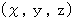 の軌跡がこの曲面を表します。
の軌跡がこの曲面を表します。

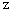 空間から
空間から 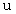

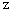 空間に座標変換すると、 次のようになります。
空間に座標変換すると、 次のようになります。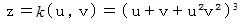


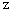 空間では、 この曲面の
空間では、 この曲面の 
 平面への正投影は全平面ではありません。 次のような十進BASIC のプログラムを実行すると、 この曲面の
平面への正投影は全平面ではありません。 次のような十進BASIC のプログラムを実行すると、 この曲面の 
 平面への正投影が描かれます。
平面への正投影が描かれます。
一方、
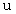

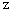 空間へ座標変換すると、 この曲面の
空間へ座標変換すると、 この曲面の 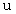
 平面への正投影は全平面になります。
平面への正投影は全平面になります。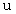

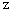 空間へ座標変換されたこの曲面の傾きは、 次のベクトルで表されます。
空間へ座標変換されたこの曲面の傾きは、 次のベクトルで表されます。
この傾きの求め方には2通りあります。 1つは、
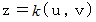 から求めるものです。
から求めるものです。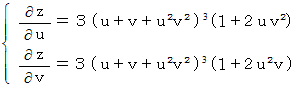
もう1つは、 合成関数から求めるものです。
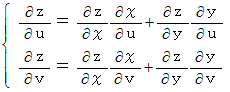
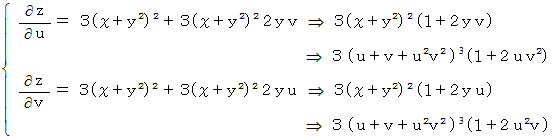
 解析学 へ戻る
解析学 へ戻る