 私見を述べます。 考えやすくするために、 光の速さを
私見を述べます。 考えやすくするために、 光の速さを  とする単位系を使用します。
とする単位系を使用します。 A君が観察するA君の座標系 ( 直交座標; 物質Bは等速直線運動している )
A君が観察するA君の座標系 ( 直交座標; 物質Bは等速直線運動している ) A君が観察するBさんの座標系 ( 斜交座標; 物質Bは静止している )
A君が観察するBさんの座標系 ( 斜交座標; 物質Bは静止している ) Bさんが観察するBさんの座標系 ( 直交座標; 物質Aは等速直線運動している )
Bさんが観察するBさんの座標系 ( 直交座標; 物質Aは等速直線運動している ) Bさんが観察するA君の座標系 ( 斜交座標; 物質Aは静止している )
Bさんが観察するA君の座標系 ( 斜交座標; 物質Aは静止している ) A君が観察するA君の座標系 ( 直交座標; 物質Aは静止している )
A君が観察するA君の座標系 ( 直交座標; 物質Aは静止している )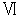 A君が観察するBさんの座標系 ( 斜交座標; 物質Aは等速直線運動している )
A君が観察するBさんの座標系 ( 斜交座標; 物質Aは等速直線運動している )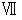 Bさんが観察するBさんの座標系 ( 直交座標; 物質Bは静止している )
Bさんが観察するBさんの座標系 ( 直交座標; 物質Bは静止している ) Bさんが観察するA君の座標系 ( 斜交座標; 物質Bは等速直線運動している )
Bさんが観察するA君の座標系 ( 斜交座標; 物質Bは等速直線運動している )ニュートン力学的座標変換であるガリレイ変換は、


 または
または 

 または
または 

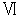 または
または 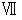

 の変換である。
の変換である。


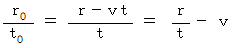


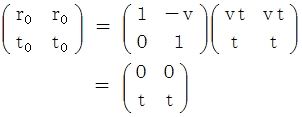


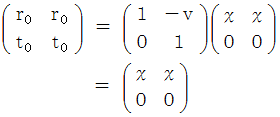

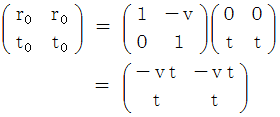


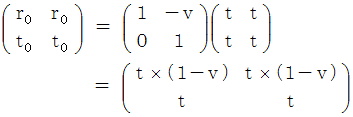

 を見ると、 ガリレイ変換後の速さがわかる。 これをニュートン力学的な速さの合成という。
を見ると、 ガリレイ変換後の速さがわかる。 これをニュートン力学的な速さの合成という。 は、 物質Bについての
は、 物質Bについての 

 のニュートン力学的な座標変換、 または、 物質Aについての
のニュートン力学的な座標変換、 または、 物質Aについての 

 のニュートン力学的な座標変換である。 これを見ると、 ガリレイ変換では、 時間は縮んだり伸びたりしないことが解る。
のニュートン力学的な座標変換である。 これを見ると、 ガリレイ変換では、 時間は縮んだり伸びたりしないことが解る。 を見ると、 ガリレイ変換では、 空間は縮んだり伸びたりしないことが解る。
を見ると、 ガリレイ変換では、 空間は縮んだり伸びたりしないことが解る。 は、 物質Aについての
は、 物質Aについての 

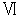 のニュートン力学的な座標変換、 または、 物質Bについての
のニュートン力学的な座標変換、 または、 物質Bについての 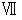

 のニュートン力学的な座標変換である。 これを見ると、 ガリレイ変換では、 時間は縮んだり伸びたりしないことが解る。
のニュートン力学的な座標変換である。 これを見ると、 ガリレイ変換では、 時間は縮んだり伸びたりしないことが解る。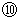 は、 光についての
は、 光についての 

 のニュートン力学的な座標変換、 または、 光についての
のニュートン力学的な座標変換、 または、 光についての 

 のニュートン力学的な座標変換である。 これを見ると、 ニュートン力学では、 座標変換によって光の速さが変化することが解る。
のニュートン力学的な座標変換である。 これを見ると、 ニュートン力学では、 座標変換によって光の速さが変化することが解る。以上のように、 ガリレイ変換によって空間や時間の長さが変化していないことが解る。 したがって、 ニュートン力学では、 第3者的見方と当事者的見方には区別は無く、 当事者的見方は第3者的見方に裏付けされているとされるのである。
ニュートン力学が比較しなければならないのは、 ガリレイ変換の前後ではない。
ニュートン力学が本当に比較しなければならないのは、 直交座標どうしの、
 と
と  または
または  と
と 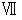 である。 2つの物質は平等に時を経るし、 規格が同じならば重さも大きさも同じである。
である。 2つの物質は平等に時を経るし、 規格が同じならば重さも大きさも同じである。また、 ニュートン力学が本当に比較しなければならないのは、 直交座標どうしの、
 と
と 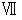 または
または  と
と  である。 1つの物質はどちらの座標系においても平等に時を経るし、 重さも大きさも同じである。
である。 1つの物質はどちらの座標系においても平等に時を経るし、 重さも大きさも同じである。また、 ニュートン力学が本当に比較しなければならないのは、 斜交座標どうしの、
 と
と 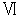 または
または  と
と  である。 2つの物質は平等に時を経るし、 規格が同じならば重さも大きさも同じである。
である。 2つの物質は平等に時を経るし、 規格が同じならば重さも大きさも同じである。また、 ニュートン力学が本当に比較しなければならないのは、 斜交座標どうしの、
 と
と  または
または 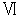 と
と  である。 1つの物質はどちらの座標系においても平等に時を経るし、 重さも大きさも同じである。
である。 1つの物質はどちらの座標系においても平等に時を経るし、 重さも大きさも同じである。相対論的座標変換であるローレンツ変換は、


 または
または 

 または
または 

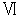 または
または 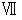

 の変換である。
の変換である。

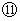
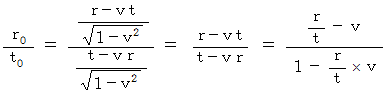

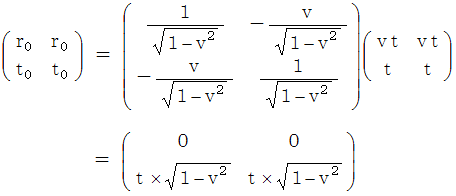

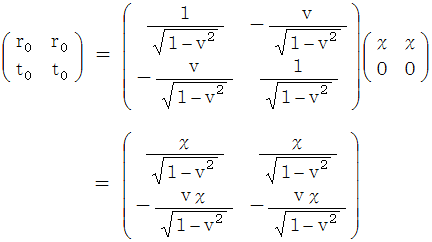

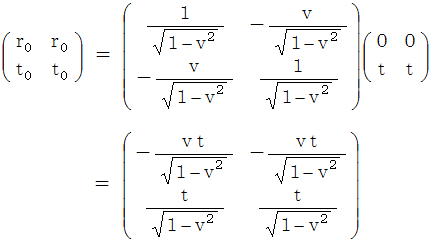

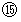

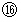
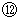 を見ると、 ローレンツ変換後の速さがわかる。 これを相対論的な速さの合成という。
を見ると、 ローレンツ変換後の速さがわかる。 これを相対論的な速さの合成という。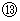 は、 物質Bについての
は、 物質Bについての 

 の相対論的な座標変換、 または、 物質Aについての
の相対論的な座標変換、 または、 物質Aについての 

 の相対論的な座標変換である。 これを見ると、 ローレンツ変換では、 時間が縮むことが解る。
の相対論的な座標変換である。 これを見ると、 ローレンツ変換では、 時間が縮むことが解る。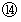 を見ると、 ローレンツ変換では、 空間が伸びることが解る。
を見ると、 ローレンツ変換では、 空間が伸びることが解る。 は、 物質Aについての
は、 物質Aについての 

 の相対論的な座標変換、 または、 物質Bについての
の相対論的な座標変換、 または、 物質Bについての 

 の相対論的な座標変換である。 これを見ると、 ローレンツ変換では、 時間が伸びることが解る。 ( 定説では、 ローレンツ変換により時間は縮みます。)
の相対論的な座標変換である。 これを見ると、 ローレンツ変換では、 時間が伸びることが解る。 ( 定説では、 ローレンツ変換により時間は縮みます。) は、 光についての
は、 光についての 

 の相対論的な座標変換、 または、 光についての
の相対論的な座標変換、 または、 光についての 

 の相対論的な座標変換である。 これを見ると、 相対論では、 座標変換によって光の速さは変化しないことが解る。
の相対論的な座標変換である。 これを見ると、 相対論では、 座標変換によって光の速さは変化しないことが解る。以上のように、 ローレンツ変換によって空間や時間の長さが変化しているのが解るが、 それはあくまで、 A君が観察する物質Bについて、 あるいは、 Bさんが観察する物質Aについて、 ニュートン力学的な第3者的見方を相対論的な当事者的見方に翻訳しただけのことであるので、 実際に空間や時間の長さが変化しているのではない。
相対性理論が比較しなければならないのは、 ローレンツ変換の前後ではない。 相対性理論が本当に比較しなければならないのは、 斜交座標どうしの
 と
と  である。 2つの物質は平等に時を経るし、 規格が同じならば重さも大きさも同じである。 ここが定説と異なる所である。 定説では、 ミューオンがゆっくりと歳を取るし、 猿の惑星のように未来へとタイムトラベルすることが出来る。 なぜなら、 定説は、 ローレンツ変換前の直交座標の
である。 2つの物質は平等に時を経るし、 規格が同じならば重さも大きさも同じである。 ここが定説と異なる所である。 定説では、 ミューオンがゆっくりと歳を取るし、 猿の惑星のように未来へとタイムトラベルすることが出来る。 なぜなら、 定説は、 ローレンツ変換前の直交座標の  と ローレンツ変換後の斜交座標の
と ローレンツ変換後の斜交座標の  とを比べるからだ。
とを比べるからだ。 ばいおりんのその他の相対論関連論文集 に戻る
ばいおりんのその他の相対論関連論文集 に戻る