湯豆腐は土鍋で作ると、 簡単に美味しく出来上がります。 木綿豆腐半丁を６等分し、 土鍋にだし昆布を敷いてその上に乗せます。 豆腐の横から水をたっぷりと注いだら、 強火にかけます。 湯が沸騰したら直ぐに弱火にして、 だし昆布を取り出し、 １分間待ちます。 火を止めた後も沸騰はしばらく続きますが心配ありません。 タレは、 ポン酢醤油とだし醤油を半々にし、 七味唐辛子と山椒を少量入れます。 土鍋はアルミ鍋に比べて熱容量が大きいので、 熱しにくく冷めにくいです。 熱容量が大きいのは、 素材の比熱が大きいためと、 質量が大きいためです。 土鍋で作った湯豆腐は、 柔らかくて最後まで温かいのです。

　 温度 と 熱 の違いはなんでしょう？　便利なインターネットで調べてみますと、「 熱とは、 熱伝達によって認識される熱エネルギーのこと。 熱エネルギーは、 温度の高い方から低い方へと伝わる。 温度とは、 内部エネルギーやエンタルピーの測定値であり、 熱伝達を生じさせる基本的動きのレベルである。 エンタルピーは、 エントロピーとは違い、 内部エネルギーに圧力と体積の積を加えたものである。 エントロピーとは、 可逆的熱機関という条件下で、 熱を温度で割ったもの。」 とあります。 しかし、 わかったようなわからいような、 なかなか難しいです。 ある系の内部エネルギーとは、 熱平衡（ 系内での熱の移動がない状況 ）下の、 分子の運動エネルギーと位置エネルギーの総和のことであり、 エンタルピーとは、 圧力一定という条件の下での熱エネルギーのことなのですが。


　 温度 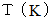とは、 ある系の 熱エネルギー 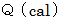を エントロピー 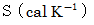で微分したものです。 微分ですから増減が関与します。 エントロピーの差は、 次のように表されます。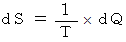
　　　　　
　 この式から、「 温度とは、 外部から系に熱エネルギーを与えた時の、 系のエントロピーの増加のしにくさを表すもの 」 とか 「 温度が高いほど、熱エネルギーを与えたときに乱雑さが増大しにくくなる。」 とか言うことができます。 温度が高い物質は、 それまでに、 外部から熱エネルギーが加えられて、 系の乱雑さがひどくなっていますので、 少々それが増えたところで、 あまり差はないのです。 一般的には、熱エネルギー量が多いと乱雑さは大きく、温度が高いと乱雑さは大きいのですが、エントロピーは熱エネルギー量や温度に比例するわけではありません。

　 熱エネルギーを加えたときに、温度は変化せずに状態が変化することがあります。 それは氷の融解です。ここにも「 エントロピー増大の法則 」が存在します。 氷の融解は見えるので、エントロピー増大のイメージとなります。

　 温度は、系の外部との境界部分に衝突する原子や分子１個の平均の運動エネルギー量を反映します。 1 秒間に外の系に衝突する分子の数を n 個 とし、 分子の平均質量を m kg とし、分子の平均衝突速度の大きさを v₀ m/s とし、 分子の平均衝突直後速度の大きさを v₁ m/s とすると、 １秒間当たりの熱伝達量は　n × 1/2 × m × ( v₀² − v₁² )　に比例します。 v₁ / v₀ は ほぼ一定でありその値を e ( 0 ＜ e ＜ 1 ) とすると、 1 秒間当たりの熱伝達量は次のような式に比例することになります。
　　　 n × 1/2 × m × v₀² × (1−e²)
したがって、 １秒間当たりの熱伝達量は温度に比例することが分かります。


　 さて、 熱容量 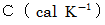とは、 物質の温度を 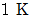上昇させるのに必要な熱エネルギーのことです。 また、 熱容量 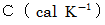は、 比熱 に質量をかけたものです。 温度の差は、 次のように表されます。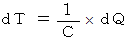
　　　　　
　 この式から、「 熱容量とは、 外部から系に熱エネルギーを与えた時の、 系の温度の上昇のしにくさを表すもの 」 と言うことができます。 これは、 一般的な熱容量の概念です。

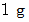　 比熱 とは、 物質 の温度を 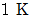上昇させるのに必要な熱エネルギーのことです。
　 ちなみに、
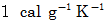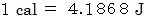　　　　水の比熱は　　です。 です。
　　　　氷の比熱は　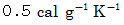　です。
　　　　水の比熱は、 水の温度によってほとんど変化しません。
　 温度を 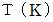、 熱エネルギー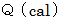を 、 質量を 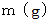とすると、 次の式が成り立ちます。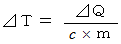
　　　　　
この式に、 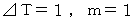を代入すると、 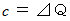になります。

また、 この式は、 次のように変形することができます。
　　　　　

　 通常の比熱を 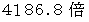したものを「 ＳＩ比熱 」と言ってはいかがでしょうか。「ＳＩ比熱 」とは、 物質 の温度を 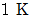上昇させるのに必要な熱エネルギー 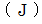です。

　 ※ 参照： 大学生のための数学 ＞ 熱力学 ＞ カルノーサイクルとエントロピー