|
階 級 |
階級値 |
度数 |
階級位 |
W1 |
W2 |
|
0 以上 20 未満 |
10 |
a |
−2 |
−2a |
4a |
|
20 以上 40 未満 |
30 |
b |
−1 |
−b |
b |
|
40 以上 60 未満 |
50 |
c |
0 |
0 |
0 |
|
60 以上 80 未満 |
70 |
d |
1 |
d |
d |
|
80 以上 100 未満 |
90 |
e |
2 |
2e |
4e |
W2 = (階級位)2 × 度数
 ヒストグラムから求めた平均の近似値 :
ヒストグラムから求めた平均の近似値 :階級位0の階級値 + 階級幅 × W1の総計 ÷ 度数の総計( 変数の数の総計 )
 ヒストグラムから求めた平均の標準偏差の近似値 :
ヒストグラムから求めた平均の標準偏差の近似値 :階級幅 × 正の平方根 {( W2の総計 ÷ 度数の総計 )−( W1の総計 ÷ 度数の総計 ) 2 }
 の式を導く :
の式を導く :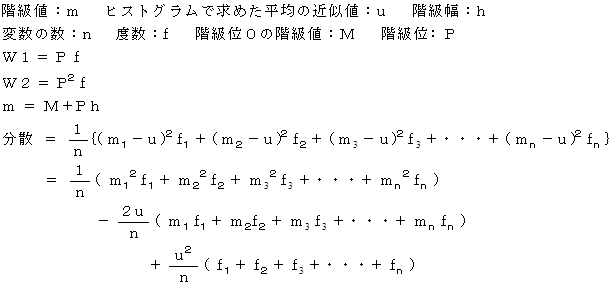
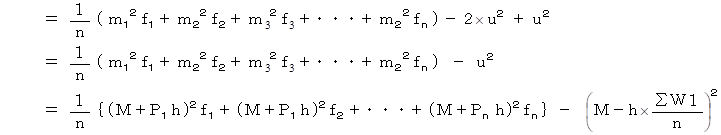
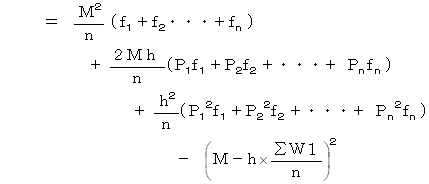
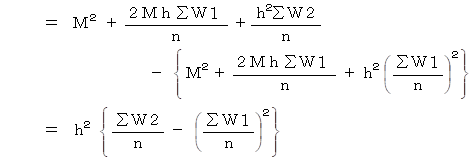
標準偏差 2 = 分散 であるから、
 の式が成り立つ。
の式が成り立つ。 統計学 へ戻る
統計学 へ戻る