【 問 題 】

（１）
　 ３次元 x y z 座標系の x z 平面上の放物線　z ＝ ４x^２ を z 軸を回転軸として１回転して出来る放物面の方程式を求めよ。


（２）
　次の範囲の各点から一斉に光子を x y 平面に対して垂直に発射したとき、全ての光子はこの放物面で反射した後に焦点 （ x，y，z ） ＝ （ ０，０，１ ） を通過するのであるが、 すべて同時に通過することを示せ。
　　　　

【 解 答 】

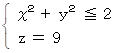
（１）
　　　　
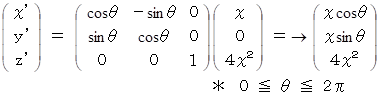
　　したがって、 回転体を表す位置ベクトルは次のようになる。
　　　　
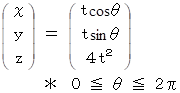
　　したがって、
　　　　


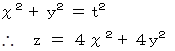
（２）
　 すべての光子が放物面では反射せずに直進すると仮定すると、 すべての光子が発射されてから　z ＝ −１ の平面までと進む距離は 10 である。 実際に放物面で反射されて光子が放物面から　z ＝ −１ の平面へと進む距離は、 光子が放物面で反射してから焦点まで進む距離に等しくなっている。 したがって、 すべての光子が放物面で反射せずに直線したと仮定すると、 すべての光子が発射されてから焦点まで進む距離は 10 である。 したがって、 すべての光子は焦点を同時に通過する。