(1) 標本平均の分布 その1
-
1000人の100点満点のテストの点数のデーターがあります。 ( data3.txt )
その平均点は 49.3120点で、 標準偏差は 14.0715点です。
その1000個のデーターからアットランダムに1個を選んでその数をメモしたら、 また1000個のデーターから1個選んでその数をメモし、 それを10回行ったら、 10回分の平均値を計算してそれを帳簿に記録します。 以上のことを2000回繰り返すと、 帳簿には平均値のデーターが2000個集まります。 そのデーターの平均と標準偏差はいくらほどになっているでしょうか?
平均値が 49.3120 ほどになっていることは予想がつきますが、 標準偏差がいくらほどになるのかは全く予想がつきません。 しかし、 それは統計学により次のようになることが知られています。
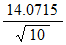
では、 十進BASI のプログラムで実験してみましょう。 次の hyouhon.bas と data3.txt を同じディレクトリーにおいてから、 十進BASIC で hyouhon.bas を呼び込んでから実行してみてください。
このプログラムソースは、 十進BASIC の生みの親である白石和夫先生のホームページよりいただきました。
http://hp.vector.co.jp/authors/VA008683/index.htm
-
母集団 { 1, 2, 3, 4, 5 } は、 件数が 5 、 平均が 3 、 標準偏差が
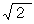 です。 この中からアットランダムに1個を取り出したときの数字を記録します。 それを2000回繰り返すと2000個のデーターが集まります。 それは、 1 〜 5 までの数がそれぞれ400個くらいになっていると思われます。 この2000件のデーターの平均は 3 で、 標準偏差は
です。 この中からアットランダムに1個を取り出したときの数字を記録します。 それを2000回繰り返すと2000個のデーターが集まります。 それは、 1 〜 5 までの数がそれぞれ400個くらいになっていると思われます。 この2000件のデーターの平均は 3 で、 標準偏差は 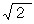 です。 その理由は次の式です。
です。 その理由は次の式です。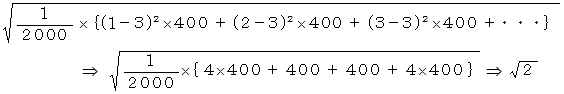
次に、 この母集団の中からアットランダムに1個を取り出してその数をメモしたら元に戻して、 またアットランダムに1個を取り出してその数をメモしたら元に戻し、 2回の平均値を帳簿に記録します。 それを2000回繰り返すと、 帳簿には2000個の平均値のデーターが集まります。
それは、
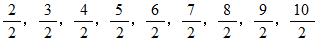 の数であり、 その度数を2000で割った値は、 順におよそ次のようになっているはずです。
の数であり、 その度数を2000で割った値は、 順におよそ次のようになっているはずです。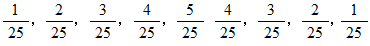
この2000件のデーターの平均は 3 で、 標準偏差は 1 です。 その理由は次の式です。
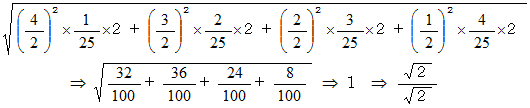
 統計学 へ戻る
統計学 へ戻る