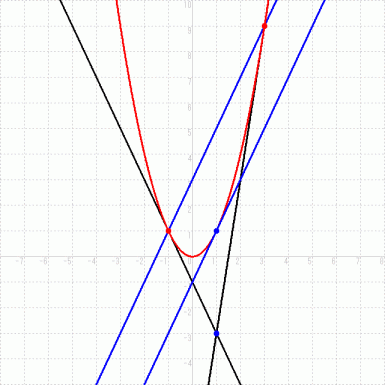
（１） ２つの点を結ぶ直線の傾き

　 x y 座標系において、 放物線上の２点を結ぶ直線の傾きは、 ２点の中点の x 座標値に対応する放物線上の点における接線の傾きに等しい。


　 放物線には上記のような法則があります。 その理由を考えてみましょう。

上記の法則は、 次のように書くことができます。
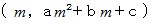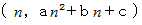　　　　 放物線上の 点　と　点 　を結ぶ直線の傾き
　　　は、 放物線上の　点 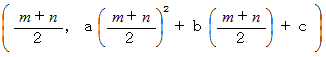における放物線の
　　　接線の傾きに等しい。

（ 参 考 ）
　　　
　　　

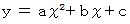
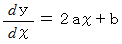
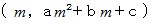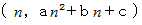点　と　点　を結ぶ直線の傾き ：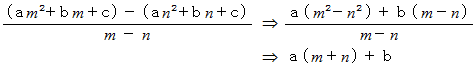
　　　　　　　

点 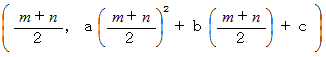　における放物線の接線の傾き ：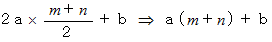
　　　　　　　

（２） ２つの接線の交点

　 x y 座標系において、 放物線上の２点における接線の交点の x 座標値は、 ２点の中点の x 座標値に等しい。


　 放物線には上記のような法則があります。 その理由を考えてみましょう。

　 簡明化目的にて、 放物線の頂点が原点となるように x y 座標系をとります。 すると、放物線の方程式は次の式で表されます。
　　　　　
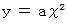
　 したがって、
　　　　　

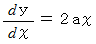
放物線上の 点 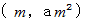における接線の方程式 ：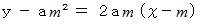
　　　　　

放物線上の 点 における接線の方程式 ：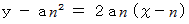
　　　　　

以上の２つの直線の交点を求めようとする ：
　　　　　辺々を引くと
　　　　　　　　　
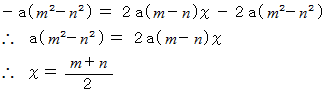
　 そういうわけで、 ２つの接線の交点の x 座標値が 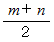であることが解りました。 とういうことは、 放物線上の２点における接線の交点の x 座標値は、 ２点の中点の x 座標値に等しいということです。

（３） その他の放物線の性質

　放物線はすべて相似である。

　頂点および最小 y 座標値が原点である放物線について言うと、 点（ ０, r )　と
　直線　y ＝ −ｒ　からの距離が等しい点は、 同一放物線上にある。

　放物線の対称軸を中心に回転してできる放物面は、 平行光線を １ つの焦点に集めることができるパラボラアンテナになる。