
(1) 1個の抽出データー
【 問 題 】
-
ある大学の男の学生の身長を調べたところ、 平均 170cm、 標準偏差 7cm であった。
身長 185cm の男の学生は身長が高いと言い切ることができるか?
有意水準 5%( 危険率 5% )で検定しなさい。
なお、 標準正規分布表より、 z > 1.96 で 全体の 2.5% 以下となります。
-
帰無仮説 : 身長 185cm の男の学生は標準的な身長である。
対立仮説 : 身長 185cm の男の学生は優位に身長が高い。
帰無仮説に従うと、無作為に抽出したデータ 185cm は、
平均 170cm、 標準偏差 7cm の正規分布の半分の 95% 範囲内にあるはずだが、
実際は、そのデーター 185cm を標準化すると、
z = ( 185 − 170 ) ÷ 7 ≒→ 2.14 となって、1.96 よりも大きい。
したがって、 帰無仮説は棄却される。
したがって、 有意水準 2.5% で、 身長 185cm の男の学生は身長が高いと言い切れる。
【 問 題 】
-
ある生産ラインの通常は、 平均注入量 50ml、 標準偏差 2.5ml である。
本日、無作為に25個のサンプルを抜き取って調べたところ、 その平均注入量は 51ml であった。
今日の生産ラインに異常があるかどうかを、 有意水準( 危険率 )5% で検定しなさい。
なお、 標準正規分布表より、 z > 1.96 で 2.5% 以下となります。
-
帰無仮説 : 今日の生産ラインは正常である。
対立仮説 : 今日の生産ラインは異常である。
帰無仮説に従うと、サンプルの平均値 51ml は、
平均 50ml、 標準偏差 2.5/root(25) ml の正規分布の 95% 範囲内にあるはずだが、
実際は、サンプルの平均値 51ml を標準化すると、次のようになる。
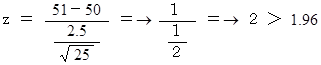
したがって、 帰無仮説は棄却される。
したがって、 有意水準 5% で、 今日の生産ラインは異常であると言い切ることができる。
 統計学 へ戻る
統計学 へ戻る