直交2次元座標系の横軸の基底の要素を
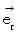 ( 実数空間 )、 縦軸の基底の要素を
( 実数空間 )、 縦軸の基底の要素を 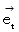 ( 虚数時間 )とします。 速さ
( 虚数時間 )とします。 速さ  で等速直線運動している慣性系への「 複素数ローレンツ座標変換 」は、 この直交2次元座標系の中に存在するある位置ベクトルを反時計回りに
で等速直線運動している慣性系への「 複素数ローレンツ座標変換 」は、 この直交2次元座標系の中に存在するある位置ベクトルを反時計回りに  ラジアン回転させる写像でもありますので、「 複素数ローレンツ座標変換 」という座標変換は、 等長変換になっていることがわかります。「 複素数ローレンツ座標変換 」は、 光の速さを
ラジアン回転させる写像でもありますので、「 複素数ローレンツ座標変換 」という座標変換は、 等長変換になっていることがわかります。「 複素数ローレンツ座標変換 」は、 光の速さを  とする単位系では、 次のように表されます。
とする単位系では、 次のように表されます。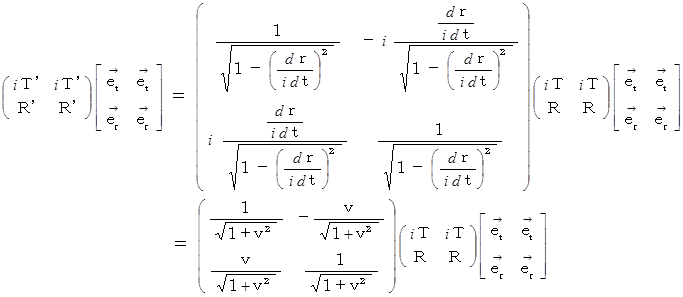
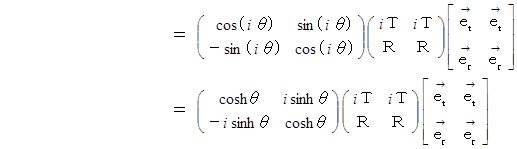
 と
と  との関係は次のようになります。
との関係は次のようになります。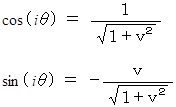
 虚数角については、 次の論文を参照にしてください。
虚数角については、 次の論文を参照にしてください。大学生のための数学 > 数理論 > 物理学における複素数の意味
大学生のための数学 > その他の数学 > 双曲線関数
大学生のための数学 > 解析学 > 双曲線関数とローレンツ座標変換
光の速さを
 とする単位系を用いて相対性理論を書き直すと、 それが理解しやすいものになるように、 時間を虚数とする「 複素数ローレンツ座標変換 」を用いて相対性理論を書き直せば、 それは理解しやすいものになると思います。 しかし、 そのために相対性理論が抱えている矛盾がなくなるわけではありません。
とする単位系を用いて相対性理論を書き直すと、 それが理解しやすいものになるように、 時間を虚数とする「 複素数ローレンツ座標変換 」を用いて相対性理論を書き直せば、 それは理解しやすいものになると思います。 しかし、 そのために相対性理論が抱えている矛盾がなくなるわけではありません。 ばいおりんのその他の相対論関連論文集 に戻る
ばいおりんのその他の相対論関連論文集 に戻る