確率 へ戻る（ 問 題 ）
-
立方体のすべての辺が東西方向または南北方向または天地方向になるように置きます。 ある頂点から出発して辺を通って対頂点 （ 対角線上の頂点 ） まで移動します。 どの辺を通って移動するのかは必ずサイコロを振って決めます。 １ または ２ が出たら東西方向の辺を通って隣の頂点に移動し、 ３ または ４ が出たら南北方向の辺を通って隣の頂点に移動し、 ５ または ６ が出たら天地方向の辺を通って隣の頂点に移動します。 対頂点まで到達するのにサイコロを振る回数は最低で３回ですが、 対頂点まで到達するのに平均で何回サイコロを振らなければならないでしょうか？
-
最低１回サイコロを振れば目的の頂点に到達できる頂点から目的の頂点に到達するまでに平均
回サイコロを振らなければならないとします。 最低２回サイコロを振れば目的の頂点に到達できる頂点から目的の頂点に到達するまでに平均 
回サイコロを振らなければならないとします。 出発点から目的の頂点まで到達するまでに平均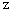 
回サイコロを振らなければならないとします。 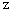， ， は期待値です。 そして、 それらには次の関係式が成り立ちます。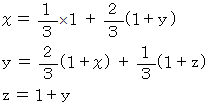
※ あと１つで頂点にいける所から失敗した場合（ 確率 2/3 ）は y になる。
つまり、 次の式たちが成り立ちます。
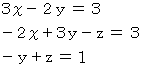
この連立３元１次方程式を解くと、次のようになります。
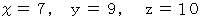
したがって、 答えは 10 回 になります。