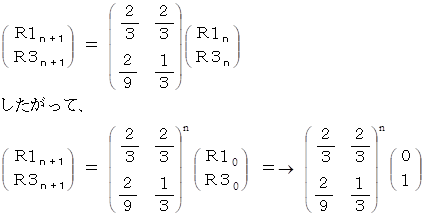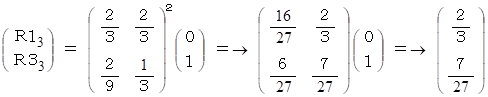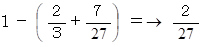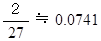頂点移動の確率漸化式
 確率 へ戻る
確率 へ戻る
 大学生のための数学 へ戻る
大学生のための数学 へ戻る
2016.12.09____
【 問 題 1 】
2つの粒子が時刻0において△ABCの頂点Aに位置している。 これらの粒子は独立に運動し、 それぞれ 1 分ごとに隣の頂点に等確率で移動していくとする。 この2つの粒子が n 分後に同じ位置にいる確率を求めよ。
( 2014年 京都大学 入試問題 より )
【 解 答 】
n が無限大の場合は、 3分の1 になりそうな予感がします。
n が 0 のときは 1 で、 n が 1 のときは 2分の1 です。
では、 問題を解いていきましょう。
n−1 分後に2点が異なる頂点に存在する場合、 n 分後に2点が同じ頂点に存在する確率は 4分の1 である。
n−1 分後に2点が同じ頂点に存在する場合、 n 分後に2点が同じ頂点に存在する確率は 2分の1 である。
したがって、 n 分後に2点が同じ頂点に存在する確率を 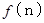 とすると、 次の式が成り立つ。
とすると、 次の式が成り立つ。
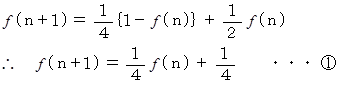
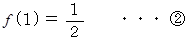
ここで、 十進BASIC で次のようなプログラムを組んで実行すると、 20分後までの各確率が解り、 それが 3分の1 に収束していくことも解ります。
OPTION BASE 0
FUNCTION f (n)
IF n=0 THEN
LET f = 1
ELSEIF n=1 THEN
LET f = 1/2
ELSE
LET f = f (n-1)/4 + 1/4
END IF
END FUNCTION
FOR i=0 TO 20
PRINT f (i)
NEXT i
END
では、 n 分後の確率 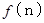 を n を用いて表せないか考えてみましょう。
を n を用いて表せないか考えてみましょう。
 は次のような式に変形することができます。
は次のような式に変形することができます。
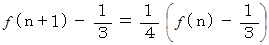
したがって、 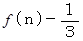 は 公比が
は 公比が 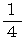 の数列です。
の数列です。
また、
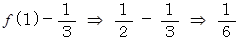
したがって、
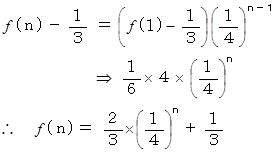
これは 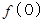 のときにも成り立っています。 この式が答えです。
のときにも成り立っています。 この式が答えです。
十進BASIC で次のようなプログラムを組んで実行すると、 答えを確かめることができます。
OPTION BASE 0
DIM f (20)
FOR i=0 TO 20
LET f (i) = 2/3*(1/4)^i + 1/3
PRINT USING "##": i;
PRINT " "; f (i)
NEXT i
END
プログラム実行結果 :
0 1
1 .5
2 .375
3 .34375
4 .3359375
5 .333984375
6 .33349609375
7 .3333740234375
8 .333343505859375
9 .333335876464844
10 .333333969116211
11 .333333492279053
12 .333333373069763
13 .333333343267441
14 .33333333581686
15 .333333333954215
16 .333333333488554
17 .333333333372138
18 .333333333343035
19 .333333333335759
20 .33333333333394
【 問 題 2 】
2つの粒子が一辺の長さが 1 cm の立方体の辺の上を 分速 1 cm で移動している。
今、 この2つの粒子とも頂点上にあってそれも最も遠い位置にある。 ( これを辺3つ分の距離ということにする。)
2.5 分後に2つの粒子が衝突する確率を求めよ。
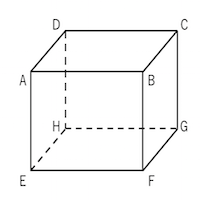
【 解 答 】
n 分後に2つの粒子は決して辺2つ分の距離になることはない。
1.5 分後以前に2つの粒子は出会うことはない。
2つの粒子が辺 1 つ分の距離のとき、 それから 1 分後に2つの粒子が出会うことなく辺 1 つ分の距離になる確率は 6 / 9 であり、 それから 1 分後に2つの粒子が出会うことなく辺3つ分の距離になる確率は 2 / 9 である。
2つの粒子が辺3つ分の距離のとき、 それから 1 分後に2つの粒子が出会うことなく辺 1 つ分の距離になる確率は 6 / 9 であり、 それから 1 分後に2つの粒子が出会うことなく辺3つ分の距離になる確率は 3 / 9 である。
n 分後に2つの粒子が出会うことなく辺 1 つ分の距離になる確率を R1n とし、 n 分後に2つの粒子が出会うことなく辺3つ分の距離になる確率を R3n とすると、
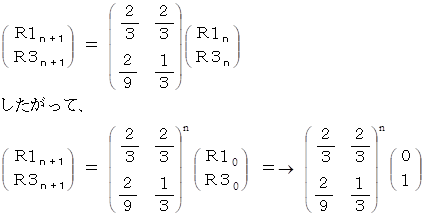
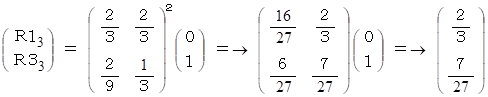
したがって、 求める答えは、
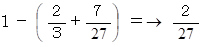
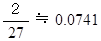
プログラム:
参考: 大学生のための数学 > 数理論 > 立方体の辺を伝わって頂点を移動する2点
 確率 へ戻る
確率 へ戻る 大学生のための数学 へ戻る
大学生のための数学 へ戻る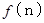 とすると、 次の式が成り立つ。
とすると、 次の式が成り立つ。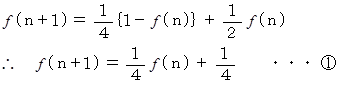
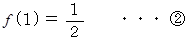
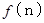 を n を用いて表せないか考えてみましょう。
を n を用いて表せないか考えてみましょう。 は次のような式に変形することができます。
は次のような式に変形することができます。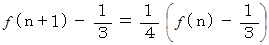
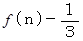 は 公比が
は 公比が 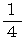 の数列です。
の数列です。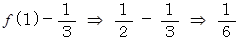
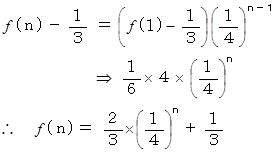
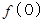 のときにも成り立っています。 この式が答えです。
のときにも成り立っています。 この式が答えです。