積分と言えば「 面積 」をイメージさせる方が多いかと思いますが、 それは、 私たちが「 関数２次元グラフ 」に慣れ親しんでいるためです。 今日は、 ３次元空間におけるスカラー場の線積分を理解していただくための、 基礎的な積分のイメージ作りについてお話したいと思います。 一般的な積分のイメージを「 微小面積総計イメージ 」としますと、 本日紹介しますのは「 微小時間キャッチ値総計イメージ 」ということになりましょうか。

　 さて、「 数直線 」とは、 １次元空間における無数の点の集まりであり、 その集まりの方向にプラスとマイナスを与えたものです。 数直線は連続か？というと、マクロ的には連続ですがミクロ的には非連続であるということができます。数直線上の隣り合う点どうしには微小な隙間があるのです。その距離を d x とします。数直線上にスカラー場が形成されているとします。 つまり、 数直線上の全ての点に d x の何倍になるかの値が与えられているとします。 その数直線上を「 掃除機能のついた点 」が移動します。 その移動のルールは、 出発点が 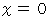であることと、 常に速さが１であること（ d t ＝ d x ）と、 過去に通過した点は通過しないことです。「 掃除機能のついた点 」は通過点を通過中に 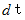の時間をかけて通過点に与えられた値をコピーして自分の体内に取り込み（ 1/2 × d t の時間では、半分しか取り込みできません。）、それを繰り返してどんどんと蓄積していきます。「 掃除機能のついた点 」は移動中に一瞬も休むことなく値を取り込んでいきます。

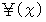　 数直線上の点の位置を とし、 その点に与えられた値を とします。 時刻を とします。「 掃除機能のついた点 」の移動のルールより、 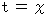です。 時刻 から 時刻 の間に、「 掃除機能のついた点 」が蓄積する値の合計は次のようになります。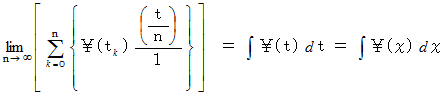

　　　　　


　 数直線上の全ての点に与えられた値がすべて である場合は、 次のような恒等式が成り立ちます。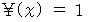
　　　　　
したがって、次の式が成り立ちます。
　　　　　
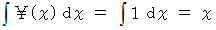
　 これは、「 掃除機能のついた点 」が時刻 から 時刻 の間に移動した道のりを表しています。


　 ３次元空間にスカラー場 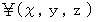が形成されており、 原点を通る曲線Ａに沿って原点から の道のりにわたって線積分をします。 先ほどの移動ルールで移動する「 掃除機能を持つ点 」を思い浮かべてください。 この曲線に沿って の時間移動させたときの「 掃除機能のついた点 」が蓄積する値の合計は次のようになります。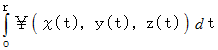
　　　　　
これが３次元空間にスカラー場の曲線Ａに従った線積分です。

　※ 参照：
　　　　 大学生のための数学 ＞ ベクトル解析 ＞ 線積分の本質
　　　　 ばいおりんの日常的物理学文集 ＞ 数学と物理学 ＞ 微小２点間距離