【 問 題 】

汁　( かつおだしの割合,　昆布だしの割合,　干し椎茸だしの割合 )
　　　　汁 A　( 90, 10, 0 )
　　　　汁 B　( 60, 30, 10 )
　　　　汁 C　( 0, 90, 10 )
　　　　汁 D　( 10, 60, 30 )
　　　　汁 E　( 10, 0, 90 )
　　　　汁 F　( 30, 10, 60 )

６人のメンバーに６種類の汁の好みの点数をつけてもらったら次のようなった。



	汁 A	汁 B	汁 C	汁 D	汁 E	汁 F	計
No.1 さんの点数	9	7	4	6	1	2	29
No.2 さんの点数	8	6	5	5	2	3	29
No.3 さんの点数	1	2	9	7	4	6	29
No.4 さんの点数	2	3	8	6	5	5	29
No.5 さんの点数	4	6	1	2	9	7	29
No.6 さんの点数	5	5	2	3	8	6	29
計	29	29	29	29	29	29	174



因子分析をして、次の３つのグループに分けよ。
　　甲グループ：　かつおだしが好き で 干し椎茸だしが嫌い な グループ
　　乙グループ：　昆布だしが好き で かつおだしが嫌い な グループ
　　柄グループ：　干し椎茸だしが好き で 昆布だしが嫌い な グループ

【 解 答 】

　この問題は、標本数が少なくてビジーでなく、また、エントロピーが低く整った形で表示されているので、因子分析をしなくても一目瞭然ですが・・・・。

行列計算：
　　

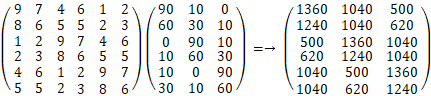
　　　　　9×90 + 7×60 + 4×0 + 6×10 + 1×10 + 2×30 ＝ 1360
　　　　　9×10 + 7×30 + 4×90 + 6×60 + 1×0 + 2×10 ＝ 1040
　　　　　9×0 + 7×10 + 4×10 + 6×30 + 1×90 + 2×60 ＝　500

　　　　　8×90 + 6×60 + 5×0 + 5×10 + 2×10 + 3×30 ＝ 1240
　　　　　8×10 + 6×30 + 5×90 + 5×60 + 2×0 + 3×10 ＝ 1040
　　　　　8×0 + 6×10 + 5×10 + 5×30 + 2×90 + 3×60 ＝　620

　　　　　　　　　　　　　　　　　　　　（ 略 ）

　　導かれた行列の
　　　　　第１行第１列は、No.1 さんの かつおだし の好みの程度を表します。
　　　　　第１行第２列は、No.1 さんの 昆布だし の好みの程度を表します。
　　　　　第１行第３列は、No.1 さんの 干し椎茸だし の好みの程度を表します。
　　　　　第２行第１列は、No.2 さんの かつおだし の好みの程度を表します。
　　　　　　　　　　　　　　　　　　　　（ 略 ）

答え：
　　甲グループ：　No.1 さん と No.2 さん
　　乙グループ：　No.3 さん と No.4 さん
　　柄グループ：　No.5 さん と No.6 さん