【 問 題 】

　 地球を半径 １ の正球とする。 地軸は公転面に対して 23.4 度 傾いているものとする。 公転面を x y 平面とし、 北半球が z 軸の正の方に存在するものとし、 地球の傾いている方向を x 軸の正の方向とし、 地球の中心を原点にとる。 北緯 Ｎ 度 の緯線が描く円の曲線上に存在するすべての点を表す位置ベクトルを求めよ。

【 解 答 】

　まず、地軸が傾いていない地球を考え、緯線の公転面に対する射影を作り、それを 23.4 度 回転させた後、 地軸の方向に提灯を広げるように広げていくことにする。
角度の単位をラジアンにするために、 次のように置く。
　　　Ｍ ＝ Ｎ × π ÷ 180
　　　Ｑ ＝ 23.4 × π ÷ 180
x y 平面上の原点を中心とする半径 １ の円の方程式は、 次のように表される。
　　　
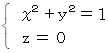
したがって、 x y 平面上の原点を中心とする半径 １ の円の曲線上に存在するすべての点を表す位置ベクトル 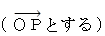は次のようになる。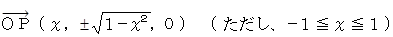
　　　
北緯 Ｎ 度 の緯線の射影が描く円の半径は、 cos М である。 そこで次のようにする。
　　　
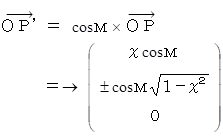
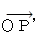を y 軸を軸として時計回りに 23.4 度 傾ける写像は次のようになる。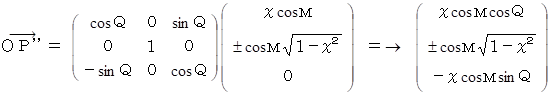
　　　
ベクトルを　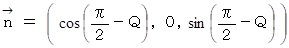　の方向に、 sin М の距離だけ平行移動させる。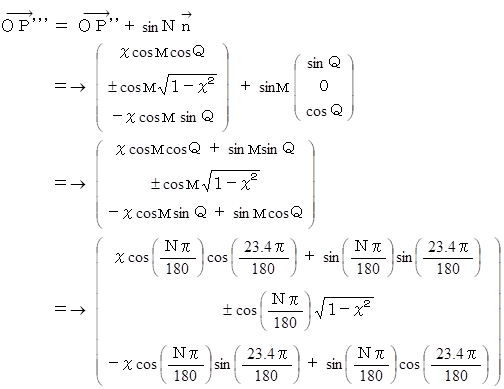
　　　
　　　　　　　　　　　　　　＊ 訂正： ＯＰ'''() ＝　ＯＰ''() ＋ sin Ｍ ｎ(→)　の間違いです。

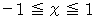として、 上記の位置ベクトルが答えとなる。