経済に代表される世の中は、心理学で動いており確率で動いているわけではありません。宝くじ や パチンコ がその証拠です。2つの封筒のパラドックスは、心理学で動いている2人を確率学の切り口で解釈すると、どこが間違っているのかを解明していく問題です。
【 問 題 1 】: 2つの封筒のパラドックスその1
-
Cさんはお金の入った2枚の封筒を手に持っています。A君にその内の1枚を選ばせて渡します。A君が自分の持っている封筒の中を見たところ ¥4000 入っていました。そしてそのことをCさんに伝えました。そこでCさんはA君に言います。「 私たちが持っている封筒の中の金額は 1:2 の比率になっています。封筒をさしあげますが、今なら交換してもいいですよ。」 Cさんが持っている封筒の中には 1/2 の確率で ¥8000 が入っています。そこで、A君は交換により獲得できる金額の期待値を計算しました。
¥8000 × 1/2 + ¥2000 × 1/2 =→ ¥5000
¥5000 > ¥4000 ですから、A君は交換を申し出ました。
今の話、怪しくありませんか? A君がどちらの封筒を選んだとしても、交換した方が得になりますよね。また、2人は永遠に交換し続けることにもなりかねません。
-
たとえば、実際にCさんが用意していたのは ¥2000 が入った封筒 と ¥4000 が入った封筒 だったのに、A君は現実に発生する可能性のない幻の ¥8000 が入った封筒 のことも考慮して期待値を求めている所がおかしいのです。「 数学的期待値 」というのは、実際に起こりうることのみで構成されなければならないので、こういった「 心理学的期待値 」を持ち出すと数学的矛盾が生じます。A君は「 幻を愛して期待したの 」のです。でも、こういうことは私たちの普段の生活の中ではよくあることです。
自分の封筒の中に ¥ 4000 が入っていることを知ったA君は、心理学的に次のように考えて封筒交換を希望します。
封筒交換によってさらに得られる金額の期待値: 1/2 × (-2000) + 1/2 × 4000 =→ 1000
確率学的にA君の心理学的考察のどこが間違いかと言うと、A君が「 2人の封筒の中の金額の合計が ¥ 6000 である確率は 1/2 で、2人の封筒の中の金額の合計が ¥ 12000 である確率は 1/2 で、どちらも現実世界で起こりうる。」と考えたことで、これを確率学的に是正すると、「2人の封筒の中の金額の合計が ¥ 6000 である確率は 1 で、2人の封筒の中の金額の合計が ¥ 12000 である確率は 1 で、どちらか一方しか現実世界では起こらない。」ということになります。そうすると、封筒交換によってさらに得られる金額の期待値は0になることがわかります。
-
Cさんはお金の入った2枚の封筒を手に持っています。A君にその内の1枚を選ばせて渡します。そしてCさんは自分が持っている封筒の中身 ¥4000 をA君に見せます。そこでCさんはA君に言います。「 私たちが持っている封筒の中の金額は 1:2 の比率になっています。封筒をさしあげますが、今なら交換してもいいですよ。」 A君が持っている封筒の中には 1/2 の確率で ¥8000 が入っています。そこで、A君は交換しないで獲得できる金額の期待値を計算しました。
¥8000 × 1/2 + ¥2000 × 1/2 =→ ¥5000
¥5000 > ¥4000 ですから、A君は交換を拒否しました。
今の話、怪しくありませんか? A君がどちらの封筒を選んだとしても、交換しない方が得になりますよね。
-
A君が持っている封筒は、現実に存在する ¥8000 が入った封筒 と ¥2000 が入った封筒 の2つの中から選んだものではない。 ¥8000 が入った封筒 と ¥2000 が入った封筒 のどちらか1つは、現実には存在しない幻の封筒なのである。期待値は現実に発生しうる確率のみから求められねばならない。なのにA君は現実に発生しない幻の確率も入れて期待値を求めている。
実存しているのは、a 円 と 2a 円 ( a = 2000 or 4000 ) がそれぞれ入っている2つの封筒だけである。4a 円 が入っている封筒は実在しないのである。
-
期待値には2種類あります。「数学的期待値」と「心理学的期待値」です。
「数学的期待値」は 現実に発生する確率のみで構成されますが、「心理学的期待値」は 幻の確率も構成要素になっています。2つの封筒のパラドックスは、確率学の切り口で見たときの心理学的期待値の矛盾を紹介しています。
「心理学的期待値」の例としては、好きな人に愛を告白して付き合ってくださいとお願いしたときに、願いが叶う確率があります。告られる彼女からするとその確率は 0% ですが、告白する彼氏にとってはその確率は 50% なのです。
「心理学的期待値」というのは、人により時により異なるものです。現状の一部分しか把握していない人にとっての「心理学的期待値」 と 現状をすべて把握している人にとっての「心理学的期待値」 とは異なるのです。また、現状のどの部分を知っているかどうかでも「心理学的期待値」は変わってきます。人間の行動は「数学的期待値」だけが根拠ではありません。「心理学的期待値」も人間の行動の根拠になります。だから、Cさんや読者はA君やB君の行動を決して批判してはならないのです。
シチュエーションその1:
-
私は太郎君と花子さんに見えない所で、Aの封筒に4000円を入れBの封筒に8000円を入れます。それから、太郎君にAの封筒を渡し花子さんにBの封筒を渡してから、2人に自分が持っている封筒の中の金額をこっそりと確認させます。そして私はこう言います。「今2人が手にしている金額は 1 : 2 の比になっています。今手にしているお金をさしあげます。ただし、今から1分以内に2人とも交換を希望した場合は交換することができます。どうしますか?」
いずれも交換によって獲得できる金額が増えることが望めるので、2人は交換をしました。2人の行動は理に適っています。しかし、私からすると、2人とも幻を期待していて滑稽です。 ( 2つの封筒のパラドックス )
-
ここに1000円札が25枚と封筒が3枚あリます。私は2人にこう言います。「太郎君、花子さん。2人とも私が目を開けてくださいと言うまで、今から目を閉じていてください。」そう言った後、コイントスして、もし表が出れば、Aの封筒に2000円を入れBの封筒に4000円を入れCの封筒に19000円を入れます。もし裏が出れば、Aの封筒に4000円を入れBの封筒に8000円を入れCの封筒に13000円を入れます。3つの封筒の中にお金を入れ終えた私は「目を開けてください。」と言います。そして、太郎君にAの封筒を渡し花子さんにBの封筒を渡します。そしてこう言います。「たった今私はコイントスをして、Cの封筒の中に入れる金額を x 円にするか y 円にするかを決め、その通りにしたところです。それから今2人が手にしている金額を 1 : 2 の比にしています。それぞれ手にしている封筒の中のお金をさしあげます。こっそりと自分の封筒の中を覗いてみてください。もし1分以内に2人とも交換を希望した場合は交換することができます。どうしますか?」
もし太郎君が2000円を持っている場合は、太郎君にとって交換によってさらに手に入れることのできる金額の期待値が500円になるので交換を希望し、もし太郎君が4000円を持っている場合は、太郎君にとって交換によってさらに手に入れることのできる金額の期待値が1000円になるので交換を希望し、もし花子さんが4000円を持っている場合は、花子さんにとって交換によってさらに手に入れることのできる金額の期待値が1000円になるので交換を希望し、もし花子さんが8000円を持っている場合は、花子さんにとって交換によってさらに手に入れることのできる金額の期待値が2000円になるので交換を希望します。いずれも交換によって獲得できる金額が増えることが望めるので、2人は交換をしました。2人の行動は理に適っています。しかし、私からすると、2人とも幻を期待していて滑稽です。 ( 2つの封筒のパラドックス )
-
1000円が入った封筒 と 2000円が入った封筒 と 4000円が入った封筒 の3枚があります。これらのお金は花子さんのものです。そのことは太郎君も知っています。ただし、花子さんはどの封筒にいくらの金額が入っているか知っていますが、太郎君は知りません。まず太郎君は無作為に1枚の封筒を選んで花子さんに渡し、残りの2枚から1枚を選んで手に取ります。すると、花子さんは自分の手にしている封筒の中のお金を太郎君に見せ、それが2000円だった場合には太郎君にこう言います。「あなたの手にしている封筒の中のお金をさしあげます。ただし1分以内にあなたの封筒を私に返してくれたら2000円さしあげます。」
太郎君は 1000円 × 1/2 + 4000 × 1/2 =→ 2500円 > 2000円 という計算をして、自分の封筒を花子さんに返さずその中のお金をもらいました。太郎君の行動は理に適っています。( 2つの封筒のパラドックスではない )
-
1000円が入った封筒 と 2000円が入った封筒 と 4000円が入った封筒 の3枚があります。これらのお金は花子さんのものです。そのことは太郎君も知っています。ただし、花子さんはどの封筒にいくらの金額が入っているか知っていますが、太郎君は知りません。まず太郎君は無作為に1枚の封筒を選んで花子さんに渡し、残りの2枚から1枚を選んで手に取ります。すると、花子さんは太郎君に封筒の中のお金を見せるように言い太郎君はそのとおりにします。それが2000円だった場合には、花子さんは太郎君にこう言います。「あなたにその2000円をさしあげます。ただし1分以内に2000円を私に返してくれたら、今私が手にしている封筒の中のお金をさしあげます。」
太郎君は 1000円 × 1/2 + 4000 × 1/2 =→ 2500円 > 2000円 という計算をして、2000円を花子さんに返して花子さんが手にしている封筒の中のお金をもらいました。太郎君の行動は理に適っています。( 2つの封筒のパラドックスではない )
【 2つの封筒のパラドックスを克服したとの勘違い 】
-
自分の封筒のお金を見たら4000円だったAさん、こう考えました。
-
私が今持っているお金は 1/4 の確率で a 円、 1/4 の確率で 2a 円、 1/4 の確率で 2a 円、 1/4 の確率で 4a 円 である。つまり、1/4 の確率で a 円、 1/2 の確率で 2a 円、 1/4 の確率で 4a 円 である。だから、交換しなかったときに私がもらえる金額の期待値は、 a×1/4 + 2a×1/2 + 4a×1/4 =→ a×9/4(円)である。
一方、私が交換をした場合にもらえる金額の期待値は次のようになる。
1/4 × 2a + 1/2 × { 1/2 × a + 1/2 × 4a } + 1/4 × 2a
=→ a/2 + 5a/4 + a/2 =→ a×9/4(円)である。
したがって、交換しようがしまいが、私が得られる金額の期待値は a×9/4 円 なのである。
a = 1000 の場合、結局は次のような式で期待値は求まる:

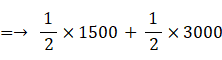
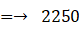
① ( 1000, 2000 )or ( 2000, 4000 )?
② 金額の少ない方を選んだ?
③ 交換した?
④ 結果的に得た金額
こう考えたAさんの考えはまともなように見えますが、実は間違っています。
封筒の中を見る前のAさんなら、こう考えるのが正しいのですけれど、Aさんは封筒の中のお金を見たわけですから、そのAさんにとって現実に存在するのは、( b, 2b )で b = a か b = 2a のどちらかであり、このどっちともが同時に実在しているわけではありません。したがって、それらを一緒くたにして確率を求めてもナンセンスです。
2つの封筒のパラドックスは「条件付き確率」に似た「条件付き期待値」の問題です。2つの封筒のパラドックスの正解は、「 1つの事象ともう1つの事象はそれぞれ 1/2 の確率でどちらも起こりうるのではなく、1つの事象ともう1つの事象はそれぞれ 1 の確率でどちらか一方しか起こらない。」です。また、2つの封筒のパラドックスから学べることは、「そのような数学的(確率学的)期待値だけで人間の行動を説明することはできない。心理学的期待値も考慮する必要がある。」ということです。
※ 参照: ばいおりんの日常的物理学文集 > 哲学と物理学 > パラレルワールドも期待するという落とし穴
( b, 2b )
集合A: b = a のとき 2b を手にしている。
集合B: b = 2a のとき b を手にしている。
★ Cさんが封筒をAさんとBさんに渡す前:
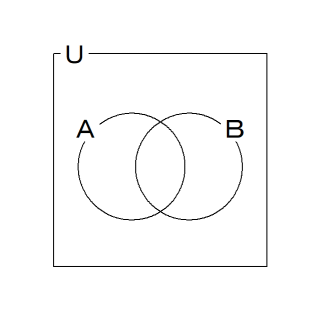
シャノン情報量: -(1/4)log2(1/4) × 4 =→ 2
★ Cさんが封筒をAさんとBさんに渡した直後:
次のどちらかに分岐収束する。
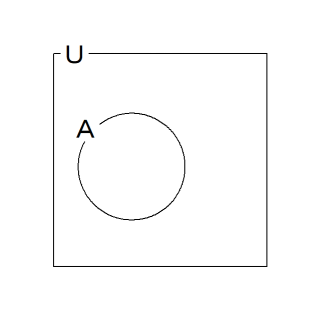
シャノン情報量: -(1/2)log2(1/2) × 2 =→ 1
シャノン情報量は、Cさんが封筒をAさんとBさんに渡したとたんに半減します。
※ 参照:
大学生のための物理学 > 基礎物理学 > 条件付き確率とエントロピー
大学生のための数学 > その他の数学 > 条件付きエントロピー
 確率 へ戻る
確率 へ戻る