等速自転座標系では、遠心力という見かけの力が発生します。このことが、無重力空間でも回転している物質にジャイロ効果が発生する原因になっています。

　　図１： 十字交差棒
　　　

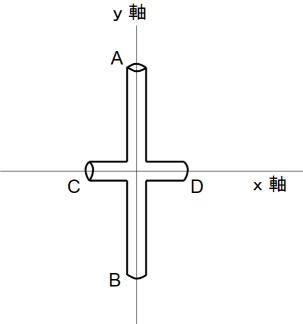
　画面に垂直方向にｚ軸を取ります。画面の手前から奥に向かう方向を正とします。

　Ｉ_ｘ： 十字交差棒のｘ軸回りの慣性モーメント
　Ｉ_ｙ： 十字交差棒のｙ軸回りの慣性モーメント
　Ｉ_ｚ： 十字交差棒のｚ軸回りの慣性モーメント
　Ｉ_ｚ ＝ Ｉ_ｘ ＋ Ｉ_ｙ
　Ｉ_ｙ ＜ Ｉ_ｘ ＜ Ｉ_ｚ

　ｘ軸のＣ→Ｄ方向に角速度を与えると、ＣＤ軸は自転的回転をし、ＡＢ軸は公転的回転をします。
　この回転に対して、もしｙ軸方向とｚ軸方向に等しい大きさの角速度を与えたとすると、ジャイロ効果によりｚ軸方向とｙ軸方向に新たな角速度が生じますが、Ｉ_ｙ ＜ Ｉ_ｚ のため、十字交差棒には主にｙ軸方向の角速度が加わるようになります。

　まず初めに、十字交差棒を少しだけ傾け、ｘ軸の正方向に角速度 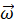を与えます。
　　図２
　　　

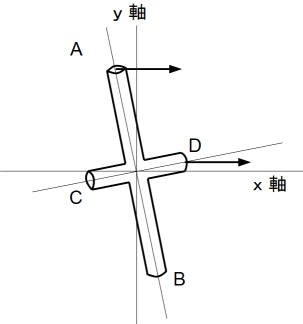
　実際は、十字交差棒の傾きは微々たるものなのですが、図ではオーバーに表現しています。
　最初は十字交差棒はｘ軸を中心に回転しますが、その後、ＣＤ軸が、ＡからＢを見つめる観察者にとって時計回りに180度公転して 遅い → 速い → 遅い と変化します。その間ＡＢ軸は、最初はｘｙ平面上を反時計回りに回転しますが、途中から時計回りになって最後は下図のように最初と反対の傾きになります。

　　図３
　　　

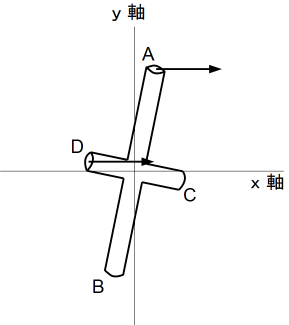
　これまでの運動を角速度 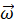を持つ 等速自転座標系で見てみる と、ＡＢ軸は全く回転してなくて（ 少しｘ軸方向に振動しますが ）、ＣＤ軸が180度公転して元の位置を入れ替えたことになります。
　この後は、十字交差棒は今までと反対の運動を行い最初の状態に戻ります。この運動の繰り返しを静止座標系の人が観察すると「ジャニベコフ効果」となります。


　これから「ジャニベコフ効果」のしくみを説明します。 図２を見てください。
　最初は、点Ａ〜Ｄはｘ座標値を一定に保ったままｘ軸を中心に回転します。
　ここで、点Ｄに作用する 遠心力 に注目します。点Ｄの位置ベクトルを 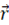とし、点Ｄには m kg の質量があるとすると、等速自転座標系では、点Ｄには 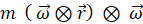で表される遠心力が作用します。向きはｙ軸の正の方向です。
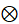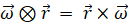　　　　　　　　　　　　　　　　　　※ 演算子 の意味は　　です。
　この遠心力はｚ軸の負の方向を向くトルク（ 力のモーメント ）を形成します。点Ｃに作用する遠心力についても同様に考えると、ｚ軸の負の方向を向くトルク（ 力のモーメント ）を形成することが分かります。
　そしてこれらのトルクは十字交差棒をｘｙ平面上を反時計回りに回転させるように働きますが、慣性モーメント（Ｉ_ｚ）が比較的大きいために少ない回転しかしません。一方、これらのトルクによって生じるこのｚ軸の負の方向を向いた新たな角速度は、 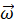に対して外積的に作用し、ｙ軸の負の方向の角速度を産生します。ジャイロ効果です。それは点Ｄをまずｚ軸の負の方向へと回転させます。点Ｄのｘ座標値が 0 になったときには、遠心力はｚ軸の負の方向を向いており、それによって生じるトルクは 0 になっています。
　新たに加わったこのｙ軸の負の方向の角速度は、 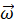に対して外積的に作用し、ｚ軸の正の方向の角速度を産生します。これは、十字交差棒をｘｙ平面上を時計回りに回転させるように働くので、十字交差棒は途中からｘｙ平面上を時計回りに回転するようになります。
　以上のＣＤ軸とＡＢ軸との協調運動により、図２から図３へと移っていきます。その後は、これまでの運動を巻き戻すようにして、図３から図２へと移っていきます。この周期的な十字交差棒の運動が「ジャニベコフ効果」です。「ジャニベコフ効果」の原理は「多重ジャイロ効果」であり、「ジャニベコフ効果」は広い意味での姿勢制御運動であります。