十進JavaScript ＋ html のプログラム：
プログラムの内容：
|
|
１位 |
２位 |
３位 |
４位 |
５位 |
６位 |
７位 |
８位 |
９位 |
10位 |
|
最 初 |
１ |
２ |
３ |
４ |
１ |
２ |
３ |
４ |
１ |
２ |
|
１回後 |
|
|
３ |
４ |
１ |
３ |
４ |
１ |
３ |
４ |
|
２回後 |
|
|
|
|
１ |
３ |
１ |
３ |
１ |
３ |
|
３回後 |
|
|
|
|
|
|
１ |
１ |
１ |
１ |
|
|
１位 |
２位 |
３位 |
４位 |
５位 |
６位 |
７位 |
８位 |
９位 |
10位 |
11位 |
|
最 初 |
１ |
２ |
３ |
４ |
１ |
２ |
３ |
４ |
１ |
２ |
３ |
|
１回後 |
|
|
|
４ |
１ |
２ |
４ |
１ |
２ |
４ |
１ |
|
２回後 |
|
|
|
|
|
|
４ |
１ |
４ |
１ |
４ |
|
３回後 |
|
|
|
|
|
|
|
|
|
１ |
１ |
では、 ここで問題です。 １ 〜
の自然数が数字格納庫の １位 から 無限大位 まで同様な状態で格納されているとき、 
番目に小さな数字格納庫に入っている数を失格として、 同様な行為を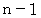 
回行った後に、 数字格納庫の中に残っている数は何でしょうか？（ 解 答 ）
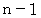回行った後に、 数字格納庫に入っている数字はすべて同じ数になります。 したがって、 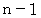回行った後に、 １番小さな数字格納庫に入っている数字が答えになります。 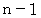回行った後に１番小さな数字格納庫に入っている数字は、 
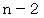回行った直後には、 が偶数の場合には最小の数字格納庫に入っている数字であり、 が奇数の場合には２番目に小さな数字格納庫に入っている数字です。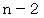 回行った直後に、 
番目に小さな数字格納庫に入っていた数は、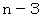 
回行った直後には、 
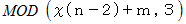番目に小さな数字格納庫に入っていました。
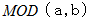は 
を 
で割った余りを出力する関数であるとします。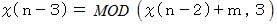
とすると、 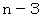回行った直後に、 
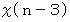番目に小さな数字格納庫に入っていた数は、 
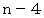回行った直後には、 
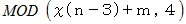番目に小さな数字格納庫に入っていました。 そこで、 
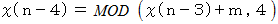と置きます。こういうふうに見ていくと、 次の式が成り立っていることがわかります。
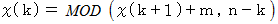
したがって、 次のようになります。
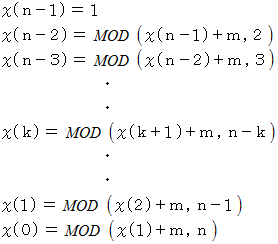
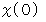の 位までの数字格納庫には数字格納庫の位と同じ数が入っていますので、 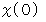が求める数字になります。ここで、
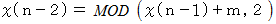についてですが、 が偶数の場合は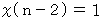 
で、 が奇数の場合は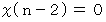 
になります。 が奇数の場合、 正しくは０番目ではなく２番目ですから、 一般的には次のように書き直さなければなりません。
こうして、 次のような十進BASIC のプログラムを組んで、 実行すれば答えがでます。
INPUT PRONPT "並べる自然数 ： １ から いくつ まで？ " : n
INPUT PRONPT "何番目に小さな数字格納庫に入った数を除外していく？ " : m
LET k = 1
FOR j = 2 to n
LET k = MOD ( k + m , j )
IF k = 0 THEN LET k = j
NEXT j
PRINT "最後に残る数は "; k ; " です。"
このプログラムは、 次のヨセフスの問題を解くプログラムと全く同じです。 ヨセフスの問題とは、 何人かの人を円形に並べておき、 ある人から時計回りに一定の順番にあたる人をOUT （ 退場 ） させたら、 その次の人からまた時計回りにその順番にあたる人をOUT させていき、 最後に残る人を当てるものです。 なお、 相対性理論に精通している人にはちょっと違和感があるかもしれませんが、 数え始める人の順番は０番ではなく１番とします。
実際に、 黒色の碁石を16個円形に並べて、 数え始める石を白石に置き換えたら、 10番目の石を取り除く行為を繰り返してみてください。 プログラムの結果と同じになります。