これはあくまでも私の夢の中の話です。 私は、 頭の上にコーヒーカップを伏せて固定し、 円形テーブルの近くに立っています。 そして、 私自身が「 自転 」したり、 あるいは円形テーブルの周囲を「 公転 」したりしています。 自分が「 自転 」することによって、 相対的に相手を「 公転 」させることができ、 自分が相手の周りを「 公転 」することによって、 相対的に相手を「 自転 」させることができます。
　「 公転 」は「 質点や剛体の重心の移動 」の１形態であり、「 自転 」は「 剛体の重心を通る直線を軸とする回転運動 」であって、「 公転 」と「 自転 」は、 物理学では異なる分野に所属しており、 その運動理論も異なります。「 地球の公転 」と言うときには、 地球を質点として捉えており、「 地球の自転 」と言うときには、 地球を剛体として捉えています。
　 惑星の公転の場合は、 公転させる力は、 回転中心に向かって作用する向心力です。 等速円運動の場合の向心力の大きさ（ ）は、 質量（ ）と 角速度（ ）と 中心から作用点までの距離（ ）を用いて、 次のように表されます。
　　　　　
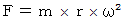
　 しかし、 公転は向心力だけで起こるわけでもありません。 その例としては、 回転するルーレーットの中を円運動する玉に見られるような「 拘束条件 」を伴う質点の移動があり、 また、 先ほどの私の夢の中の私の行動のようなケースもあります。
　 自転や公転は合成することができ、 このことを「 自転公転の相対原理 」と私は言っています。
　　　　　　　※ 参考：　剛体力学 ＞ 自転公転の相対原理

　 地球は、「 公転 」とは独立した「 自転 」をしながら、 太陽の周りを公転しています。 月は、「 公転 」の角速度と同じ大きさの角速度ベクトルで「 自転 」をしながら、 地球の周りを公転しています。 月の誕生は、 地球と惑星の衝突から始まります。 衝突により粉々になった惑星と地球の一部は、 次第に２手に分かれてくっついていきます。 一つは地球に、 もう一つは破片どうしで。 そして後者は月になりました。 このような過程をふんでいるので、 月は「 公転 」と同じ角速度の「 自転 」をしながら、 地球の周りを公転するようになったものと思われます。 それゆえ、 月は地球に対していつも同じ面を向けています。 月が地球の周りを１公転したときには、 月は１自転しています。

　 ２次元空間において、 ３角形が反時計回りに回転しているとします。 回転中心は３角形の重心かもしれませんし、 はたまた、 ３角形の外部にある存在するかもしれません。 ３角形内の各点は回転中心の方を向いたまま回転していると考えてください。 つまり、３角形が１回転したときには、 ３角形の内部のある微小部分は、 その回転中心の周りを１公転したことになると共に、 １自転したことになります。

　 剛体の回転運動でも、 剛体が重心を通る軸あるいはそうでない軸を回転中心として１回転したときには、 剛体の内部のある微小部分は、 その回転中心の周りを１公転したことになると共に、 １自転したことになります。「 剛体の内部の微小部分の公転・自転 」は 剛体の回転に属する現象です。

　「 剛体の回転 」は、 大きさとしての「 単位時間あたりの回転角度 」と、 方向としての「 回転面に対する右ネジの法則による垂直方向 」とで表現され、 それは「 角速度 」と言われます。 このように定義することができるのは、 ベクトルの起点を含みそのベクトルに垂直な平面は１つだけ存在するからです。「 力のモーメント 」もその方向は「 回転面に対する右ネジの法則による垂直方向 」なのですが、「 角速度 」は「 力のモーメント 」とは異なります。 また、「 角速度 」は「 不均一流速内水車回転作用（ ベクトル場の回転 ）」とも異なります。

　 ３次元空間において自転している地球でも、 地球内の各点は同一の「 角速度 」の公転と自転とをしています。 その向きは北向きであり、 その大きさは次のようになっています。
　　　　

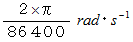
　「 角速度 」は回転中心の位置の情報を持ちません。 したがって、「 角速度 」からは「 自転 」なのか「 公転 」なのかを区別することはできません。

　「 角速度 」は、 合成や分解をすることができます。 それは「 歯車による回転伝達機構 」のような角速度を変換して伝達するのとは異なります。 その例をいくつか見てみることにしましょう。

　 １番目は、「 剛体の自転と剛体の自転の合成の例 」です。 床に対して角速度の大きさ で自転しているターンテーブルの中央と片隅にコーヒーカップが１つずつ置いてあり、 それらはターンテーブルに対して角速度の大きさ で自転しています。 これらのコーヒーカップは、 ターンテーブルが床に対して１自転する間に、 床に対して２自転します。 なぜなら、 ターンテーブルのコーヒーカップが置かれた所の局所面は、 床に対して角速度の大きさ で自転しているからです。 コーヒーカップの床に対する自転は、「 角速度 」の合成式で表すと、 次のようになります。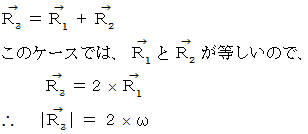
　　　　

　 ２番目は、「 剛体の自転と質点の公転の合成の例 その１ 」です。 床に対して角速度の大きさ で自転しているターンテーブルの中央近くにコーヒーカップが置いてあり、 それは、ターンテーブルに対して角速度の大きさ でターンテーブルの中心を回転中心として公転すると共に、ターンテーブルに対して角速度の大きさ で自転しています。 このコーヒーカップは、 ターンテーブルが床に対して１回自転する間に、 床に対して２回公転し、２回自転します。なぜなら、ターンテーブルが床に対して１回自転する間に、 ターンテーブル上のコーヒーカップの軌道は１回公転し１回自転するので、公転と自転に関してそれぞれ次の「 角速度 」の合成式が成り立つからです。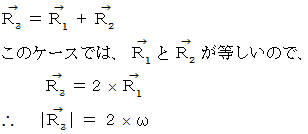
　　　　
本当は、「 公転 」と「 自転 」とは運動形態が違うのですが、 「 角速度 」の合成をすることができるのです。

　 ３番目は、「 剛体の自転と質点の公転の合成の例 その２ 」です。 床に対して角速度ベクトルの大きさ で自転しているターンテーブルの片隅で、 コーヒーカップがターンテーブル上のある点を中心にして小さな円を描いて、 ターンテーブルに対して角速度の大きさ で公転すると共に、ターンテーブルに対して角速度の大きさ で自転しています。 このコーヒーカップは、 ターンテーブルが床に対して１回自転する間に、 床に対して１回公転（ ふらふらしながらの公転です。）し、２回自転します。