ひっそりと生きているものの立場から、 ものを見ることのできた みすゞ です。


（２）　自転公転の相対原理 （ 私の造語です ）

　自転公転の相対原理 ：

　　観察者にとっての被観察物質の自転の角速度 ：
　　　　　　被観察物質が観察者の回りを公転している場合 ：　ω_YJ − ω_IJ
　　　　　　観察者が被観察物質の回りを公転している場合 ：　ω_YJ − ω_IJ

　　観察者にとっての被観察物質の公転の角速度 ：
　　　　　　被観察物質が観察者の回りを公転している場合 ：　ω_YK − ω_IJ
　　　　　　観察者が被観察物質の回りを公転している場合 ：　ω_IK − ω_IJ＿＿

　　　　　　　　　　　　　　 ω_IJ ：　観察者の自転の角速度
　　　　　　　　　　　　　　 ω_IK ：　観察者の公転の角速度
　　　　　　　　　　　　　　 ω_YJ ：　被観察物質の自転の角速度
　　　　　　　　　　　　　　 ω_YK ：　被観察物質の公転の角速度

　※　観察される 公転 や 自転 は、実際の 公転 や 自転 から観察者の自転を引いたものになっている。＿＿
　※　観察される自転については、公転は一切関係ない。

（３）　地球から見た太陽

　 地球にとっての太陽の相対的公転周期がちょうど １ 日になることを確かめまてみましょう。
　　　　　地球の公転周期 ：　
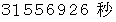
　　　　　地球の自転周期 ：　　　
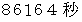
　ω_YK + ω_IK − ω_IJ　の式にあてはめると、 次のようになります。
　　　　　
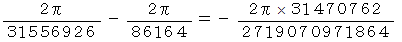
　 １ 回転する時間とは、 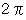ラジアン回転する時間のことですので、 １ 回転する時間は、 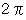を角速度で割れば出ます。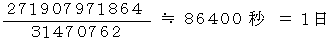
　　　　　

　 地球にとっての太陽の相対的公転周期と、 太陽にとっての地球が １ 自転する時間とは同じです。


（４）　月から見た地球

　 常に地球が見える側の月面に寝転がっている人からは、 地球はどう見えるでしょうか。
　　　　　地球の自転周期 ：　　
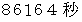
　　　　　月の自転周期 ：　
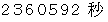
　　　　　月の公転周期 ：　

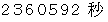
　 月は自転と公転のスピードと向きが同じです。 したがって、 月から地球を見れば、 地球は公転せずに同じ位置に止まっています。 （ 地球の入り や 地球の出 は ありません。） このことは ω_YK + ω_IK − ω_IJ　の式からも分かります。 月からすると地球は 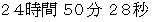の周期で自転しています。 これは地球から見たときの月が地球を回る周期と同じです。

　　　　＊ コメント ；　月から見たときの地球が １ 自転する時間 の求め方
　　　　　　　ω_YJ − ω_IJ　の式に当てはめて、
　　　　　　　　　　
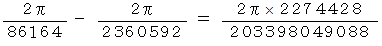
　　　　　　　１ 自転する時間は、 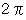を角速度で割ればいいので、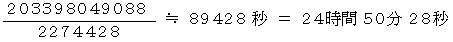
　　　　　　　　　　

　 また、 地球の大きさは 月の 約 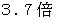ですので、 新月の月からは、 満月の 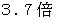の青い丸い地球を見ることができます。


（５）　地球から見た月

　 地球から見る月も自転しています。 と言うと、 「 ウソでしょう！　その証拠に月の裏側を見た人はいません。」 という反論が返って来そうです。 そこで、 「 月は、 平面上で円が回転するように自転しています。」 と申し上げます。 そして、 「 それを理解するためには、 ２個のコインを机上で回転させてはいけません。 両手で １ 個ずつ持って３次元空間の中で回転させてください。」 と申し上げます。

　　　　　地球の自転周期 ：　　
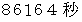
　　　　　月の自転周期 ：　

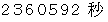
　 地球から見たときの月が １ 自転する時間 の求め方 ：
　　　　　ω_YJ − ω_IJ　の式に当てはめて、
　　　　　　　　　　
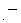
　　　　　１ 自転する時間は、 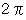を角速度で割ればいいので、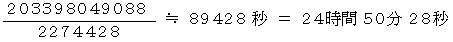
　　　　　　　　　　


（６）　考えやすくするための、 自転 と 公転 の設定

　自転 ：

　 xｙｚ座標からなる３次元座標系を設置し、 ｚ軸を中心にしてｚ軸から原点に向かう方向から見て反時計回りに座標が回転している状況を自転とする。

　公転 ：

　 xｙｚ座標からなる２つの３次元座標系ＡとＢとを設置し、 ｚ軸は同じ向きで、 ２つの座標系のxｙ平面は同一平面となっているものとする。 座標系Ａの原点を中心にして座標系Ｂの原点が、 座標系Ａのｚ軸から原点に向かう方向から見て反時計回りに回転している状況を公転とする。

　 座標系Ａの原点には 「 身体の向きを変えなくとも同時に四方八方を見渡すことのできる観察神 」 が存在し、 座標系Ｂの原点には玉が存在する。 以上のような設定において、 次の４つの思考実験を行う。

　１．

座標系Ａの自転の角速度の大きさ （ ω_Ａj ）　＝　０
座標系Ｂの公転の角速度の大きさ （ ω_Ｂk ）　＝　０
座標系Ｂの自転の角速度の大きさ （ ω_Ｂj ）　＝　ω （ ω ＞ ０ ）
このとき、 観察神が １ / ω 以上の時間をかけて玉を観察すれば、 玉の表面をすべて見ることができる。

　２．

座標系Ａの自転の角速度の大きさ （ ω_Ａj ）　＝　ω （ ω ＞ ０ ）
座標系Ｂの公転の角速度の大きさ （ ω_Ｂk ）　＝　ω
座標系Ｂの自転の角速度の大きさ （ ω_Ｂj ）　＝　０
このとき、 観察神が １ / ω 以上の時間をかけて玉を観察すれば、 玉の表面をすべて見ることができる。
観察神にとっての玉の自転の角速度の大きさ　＝　ω_Ｂj − ω_Ａj　＝　−ω
観察神にとっての玉の公転の角速度の大きさ　＝　ω_Ｂk − ω_Ａj　＝　０

　３．

座標系Ａの自転の角速度の大きさ （ ω_Ａj ）　＝　ω （ ω ＞ ０ ）
座標系Ｂの公転の角速度の大きさ （ ω_Ｂk ）　＝　ω
座標系Ｂの自転の角速度の大きさ （ ω_Ｂj ）　＝　ω
このとき、 観察神はいくら時間をかけても玉の表面の半分しか見ることができない。
観察神にとっての玉の自転の角速度の大きさ　＝　ω_Ｂj − ω_Ａj　＝　０
観察神にとっての玉の公転の角速度の大きさ　＝　ω_Ｂk − ω_Ａj　＝　０

　４．

座標系Ａの自転の角速度の大きさ （ ω_Ａj ）　＝　０
座標系Ｂの公転の角速度の大きさ （ ω_Ｂk ）　＝　ω （ ω ＞ ０ ）
座標系Ｂの自転の角速度の大きさ （ ω_Ｂj ）　＝　ω
このとき、 観察神はいくら時間をかけても玉の表面の半分しか見ることができない。

　 実験３は、 観察神は静止している玉をずっと見ている状況である。
　 実験４は、 観察神にとって玉は同じ面をずっと向けながら自転している状況である。

さらに２つの思考実験を行う。

　５．

座標系Ａの自転の角速度の大きさ （ ω_Ａj ）　＝　Ω （ Ω ＞ ０ ）
座標系Ｂの公転の角速度の大きさ （ ω_Ｂk ）　＝　ω （ ω ＞ ０ ）
座標系Ｂの自転の角速度の大きさ （ ω_Ｂj ）　＝　ω
このとき、 観察神はいくら時間をかけても玉の表面の半分しか見ることができない。
観察神にとっての玉の自転の角速度の大きさ　＝　ω_Ｂj − ω_Ａj　＝　ω − Ω
観察神にとっての玉の公転の角速度の大きさ　＝　ω_Ｂk − ω_Ａj　＝　ω − Ω

　６．

座標系Ａの自転の角速度の大きさ （ ω_Ａj ）　＝　０
座標系Ｂの公転の角速度の大きさ （ ω_Ｂk ）　＝　ω − Ω
座標系Ｂの自転の角速度の大きさ （ ω_Ｂj ）　＝　ω − Ω
このとき、 観察神はいくら時間をかけても玉の表面の半分しか見ることができない。

　 実験６は、 実験５を観察神の立場に立って記述したものである。
　 実験６は、 実験４と角速度の大きさが異なるだけである。
　 ２つの追加思考実験をした目的は、 満月の兎が自転していることを理解するためである。

備考 ：
　 月が同じ面を見せながら自転しているのは、 月の自転軸が変化したためではありません。 月は地球の自転と反対方向に相対的に自転しているのですが、 相対的公転のために地球からの位置を変えているので、 そのように見えるのです。 月の自転軸は兎に対して横向きになっています。


（７）　追伸

　 一般的には 「 月は地球からすると自転していない。」 と間違って考えられていますが、 それは、 公転の中心で惑星の公転の角速度と同じ角速度で自転している観察者の立場で観察した結果のことを言っているからです。 しかし、 客観的な見方にするためには、 公転の中心で自転していない観察者の立場で観察しなければなりません。 観察神になりきって観察しなければなりません。